Задание № 21039
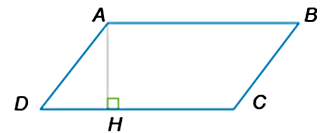
Сторона AB параллелограмма ABCD равна 20, а периметр параллелограмма равен 60. Найдите длину отрезка DH (где H — основание высоты AH), если диагональ AC=10√3.
Решать другие задания по теме: Планиметрия
Показать ответ
Комментарий:
Так как стороны параллелограмма попарно равны, то AD=P/2—AB=60/2—20=10. По теореме косинуса находим угол D:
[math]\cos\left(\angle D\right)=\frac{AD^2+DC^2-AC^2}{2\cdot AC\cdot DC}=\frac{10^2+20^2-(10\sqrt3)^2}{2\cdot10\cdot20}=0,5[/math]
Косинус этого же угла в прямоугольном треугольнике равен cos D=DH/AD, значит DH=AD⋅cos D=5
Ответ: 5Нашли ошибку в задании? Выделите фрагмент и нажмите Ctrl + Enter.