Вариант 3
Математика Базовый уровень
Ответом к каждому заданию является конечная десятичная дробь, целое число или последовательность цифр. Запишите ответы к заданиям в поле ответа справа от номера соответствующего задания. Если ответом является последовательность цифр, то запишите эту последовательность без пробелов, запятых и других дополнительных символов. Каждую цифру, знак «минус» и запятую пишите в отдельной клеточке в соответствии с приведёнными в бланке образцами. Единицы измерений писать не нужно.
Найдите значение выражения (1,12−0,31)⋅0,3.
Найдите значение выражения [math]\frac{22^{-7}\cdot11^7}{\left(2^4\right)^{-2}}[/math].
В первой четверти Андрей получил 20 пятерок по математике, а во второй — только 13 пятерок. На сколько процентов уменьшилось количество пятерок у Андрея во второй четверти по сравнению с первой?
Среднее геометрическое трёх чисел a, b и c вычисляется по формуле [math]d=\sqrt[3]{abc}[/math]. Найдите среднее геометрическое чисел 27, 2 и 4.
Найдите значение выражения [math]144^{\log_93}[/math].
В коробку вмещаются 17 пачек конфет. Определите, какое наименьшее количество коробок потребуется кондитерской фабрике, чтобы разложить 746 пачек изготовленных конфет.
Найдите корень уравнения: 0,83x−1=1,25.
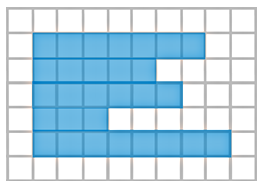
План местности разбит на клетки. Каждая клетка обозначает квадрат 1 м х 1 м. Найдите площадь участка, изображённого на плане. Ответ дайте в квадратных метрах.
Установите соответствие между величиной (обозначено буквами) и её возможным значением (обозначено цифрами).
| ВЕЛИЧИНЫ | ВОЗМОЖНЫЕ ЗНАЧЕНИЯ |
| А) длина футбольного поля | 1) 18 см |
| Б) длина автомобиля | 2) 345 см |
| В) длина карандаша | 3) 106 м |
| Г) длина экватора Земли | 4) 40 075,7 км |
В вагоне метрополитена находятся 150 человек, 123 из которых направляются на работу. Найдите вероятность того, что один случайно выбранный человек из данного вагона не едет на работу.
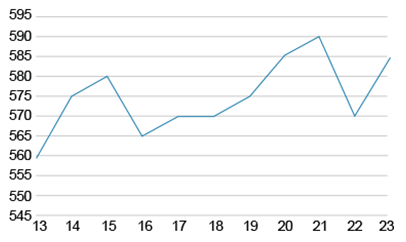
На рисунке изображен график изменения стоимости акций производственного предприятия с 13 по 23 октября 2016 года. По горизонтали указана дата, по вертикали — стоимость 1 акции в данный день (в руб.). Определите по графику, в течение скольких дней из представленного периода стоимость одной акции была не более 580 рублей.
В таблице указаны цены (в руб.) на услуги авиаперевозки пассажиров экономического класса по маршруту Москва — Рим четырех разных авиакомпаний.
| Авиакомпания | Стоимость билета | Стоимость провоза багажа | Стоимость питания на борту |
| Аэродруг | 8500 | Бесплатно | Бесплатно |
| Эйр Хэппи | 3400 | 3000 | 1000 |
| Полёт | 3500 | 2500 | 700 |
| Крылья | 6500 | Бесплатно | 500 |
Определите, сколько рублей нужно заплатить за самый дешевый билет, если путешественник планирует сдать багаж и заказать питание на борту.
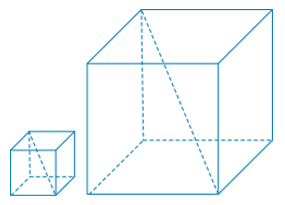
Площадь поверхности некоторого куба равна 12 м2. Найдите площадь поверхности куба (в м2), диагональ которого в три раза больше диагонали данного куба.
На рисунке изображён график функции y=f(x). Точки a, b, c, d и e задают интервалы на оси Ox.
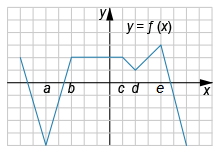
Пользуясь графиком, поставьте в соответствие каждому интервалу (обозначено буквами) характеристику функции и ее производной (обозначено цифрами).
| Интервал | Характеристика |
| А) (a; b) | 1) Значения производной функции отрицательны. |
| Б) (b; c) | 2) Значения функции положительны. |
| В) (c; d) | 3) Производная функции равна нулю на всем промежутке. |
| Г) (d; e) | 4) Значения производной функции положительны. |
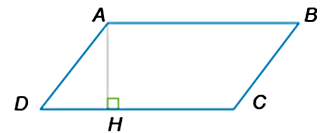
Сторона AB параллелограмма ABCD равна 20, а периметр параллелограмма равен 60. Найдите длину отрезка DH (где H — основание высоты AH), если диагональ AC=10√3.
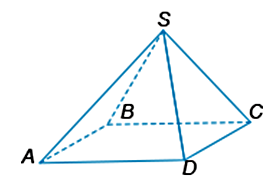
Сторона основания правильной четырехугольной пирамиды SABCD равна 5√2 м. Найдите высоту пирамиды (в м), если известно, что боковые рёбра наклонены к плоскости основания под углом 45∘.
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенством (обозначено буквами) и его решением (обозначено цифрами).
| Неравенство | Решение |
| А) x2≤144 | 1) (−∞; +∞) |
| Б) x2≥−144 | 2) нет решений |
| В) x2≤−144 | 3) [−12; 12] |
| Г) x2≥144 | 4) (−∞; −12]∪[12; +∞) |
Андрей купил в магазине одежды футболку, рубашку, джинсы и сумку. Известно, что рубашка дороже футболки, джинсы дороже рубашки, а сумка стоит дешевле джинсов. Выберите утверждения, которые верны для приведенных данных.
1) Джинсы стоят дороже футболки.
2) Футболка — самая дешевая из всех вещей.
3) Среди покупок нет двух вещей с одинаковой стоимостью.
4) Джинсы — самая дорогая вещь из купленных.
Приведите пример такого трехзначного числа, которое при делении на 29 и 31 даёт равные ненулевые остатки, и первая цифра которого в три раза больше последней цифры.
В лотке 30 яиц: белые и рябые. Известно, что среди любых 12 яиц имеется хотя бы одно рябое, а среди любых 20 яиц — хотя бы одно белое. Сколько белых яиц в лотке?
| № | Ваш ответ | Ответ и решение | Первичный балл |
|---|---|---|---|
|
Здесь появится результат первой части. Нажмите на кнопку «Завершить работу», чтобы увидеть правильные ответы и посмотреть решения. |
|||