Решение:

а) Диагонали квадрата перпендикулярны, поэтому [math]\mathrm{AC}\perp\mathrm{BD}[/math] (см. рисунок) С другой стороны, так как пирамида правильная вершина [math]\mathrm S[/math] проецируется в центр основания, поэтому основание высоты и точка пересечения диагоналей квадрата [math]\mathrm{ABCD}[/math] совпадают. Обозначим эту точку [math]\mathrm O[/math], плоскость [math](\mathrm{SAO})\perp\mathrm{BD}[/math], так как содержит 2 пересекающиеся прямые, перпендикулярные BD. Сечение плоскостью [math]\mathrm{AOS}[/math] образует [math]\bigtriangleup SAC[/math], так как точки [math]A,O,C[/math] лежат на одной прямой.

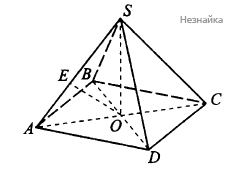
б) Обозначим через [math]O[/math] точку пересечения диагоналей квадрата. Диагональ [math]AC\perp BD[/math] и высота пирамиды [math]SO\perp BD[/math], поэтому [math]BD\perp AOS[/math]. Пусть [math]E[/math] - основание перпендикуляра, опущенного из точки [math]O[/math] на ребро SA. Так как [math]BD\perp AOS[/math], то [math]BD\perp OE[/math]

Таким образом, [math]OE[/math] - общий перпендикуляр к скрещивающимся прямым [math]BD[/math] и [math]SA[/math]. Заметим, что [math]OE[/math] - высота прямоугольного треугольника [math]AOS[/math], опущенная на гипотенузу [math]AS[/math]. Пусть [math]AO=a[/math] , тогда [math]SO=\sqrt{25-a^2}[/math]. Площадь треугольника [math]AOS[/math] равна [math]\frac12SA\times OE=5[/math], с другой стороны равна [math]\frac12AO\times SO=\frac12a\sqrt{25-a^2}[/math]. Решим уравнение [math]\frac12a\sqrt{25-a^2}=5[/math]. Оно имеет положительные корни [math]a=\sqrt5,\;a=2\sqrt5[/math]

Пусть [math]a=\sqrt5[/math], тогда [math]SO=2\sqrt5[/math] и площадь основания данной пирамиды равна [math]\frac12(2a)^2=10[/math]. Объем пирамиды [math]SABCD[/math] равен [math]\frac13\times10\times2\sqrt5=\frac{20\sqrt5}3[/math]

Пусть [math]a=2\sqrt5[/math], тогда [math]SO=\sqrt5[/math] и площадь основания данной пирамиды равна [math]\frac12(4\sqrt5)^2=40[/math]. Объем пирамиды [math]SABCD[/math] равен [math]\frac13\times40\times\sqrt5=\frac{40\sqrt5}3[/math]

Ответ: [math]\frac{20\sqrt5}3[/math] и [math]\frac{40\sqrt5}3[/math]