Задание № 7904
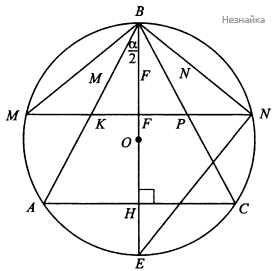
Равнобедренный треугольник АВС вписан в окружность радиуса R, ∠АВС = α. Параллельно основанию АС проведена средняя линия, продолженная до пересечения с окружностью в точках М и N.
а) Докажите, что [math]AB=2R\cos\frac\alpha2[/math]
б) Найдите отношение площади треугольника MBN к площади треугольника АВС, если ∠АВС = 60°
а) В [math]\bigtriangleup ABC[/math] по теореме синусов [math]\frac{AC}{\sin\angle ABC}=2R,\;AC=2R\sin\alpha[/math]
Проведем [math]BH\perp AC[/math]
По условию [math]\bigtriangleup ABC[/math] - равнобедренный, значит высота [math]BH[/math] является медианой и биссектрисой [math]AH=\frac12AC=R\sin\alpha[/math] (см. рисунок)
[math]AB=\frac{AH}{\sin{\displaystyle\frac\alpha2}}=\frac{R\sin\alpha}{\sin{\displaystyle\frac\alpha2}}=2R\cos\frac\alpha2[/math], что и требовалось доказать.
б) В [math]\bigtriangleup ABH\;tg\angle ABH=\frac{AH}{BH}[/math], [math]\;BH=\frac{AH}{tg\angle ABH}=\frac{R\sin\alpha}{tg{\displaystyle\frac\alpha2}}=2R\cos^2\frac\alpha2=2R\cos^230^\circ=\frac32R[/math]
По условию [math]KP[/math] - средняя линия [math]\bigtriangleup ABC[/math], значит, [math]BF=\frac12BH=\frac34R.[/math]
[math]\angle BNE=90^\circ[/math], как вписанный опирающийся на диаметр, следовательно [math]\bigtriangleup BNE[/math] - прямоугольный.
По свойству высоты, проведенной из вершины прямого угла, [math]NF^2=BF\times FE=\frac34R\times(2R-\frac34R)=\frac{15}{16}R^2[/math]
[math]NF=\frac{\sqrt{15}R^2}4[/math], [math]MN=2NF=\frac{R\sqrt{15}}2[/math]
[math]\begin{array}{l}S_{MBN}=\frac12MN\times BF=\frac12\times\frac{R\sqrt{15}}2\times\frac34R=\frac{3\sqrt{15}}{16}R^2\\S_{ABC}=\frac12AB\times BC\times\sin\angle ABC=\frac12\times(2R\cos\frac\alpha2)^2\times\sin\alpha=\frac{3\sqrt3}4R^2\\\frac{S_{MBN}}{S_{ABC}}=\frac{3\sqrt{15}R^2}{16}\div\frac{3\sqrt3}4R^2=\frac{\sqrt5}4\end{array}[/math]
Ответ: [math]\frac{\sqrt5}4[/math]
Нашли ошибку в задании? Выделите фрагмент и нажмите Ctrl + Enter.