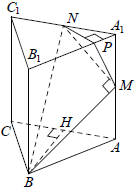
Пусть точка H — середина AC. Тогда

[math]BN^2=BH^2+NH^2=(3\sqrt3)^2+6^2=63[/math]

Вместе с тем,

BM² + MN² = (3² + 6² ) + (3² + 3² ) = 63, а тогда по теореме, обратной теореме Пифагора, треугольник BMN является прямоугольным с прямым углом M.

Проведём перпендикуляр NP к прямой A₁B₁.

Тогда NP [math]\perp[/math] A₁B₁ и NP [math]\perp[/math] A₁A. Следовательно, NP [math]\perp[/math] ABB₁ . Поэтому MP — проекция MN на плоскость ABB₁.

Прямая BM перпендикулярна MN , тогда по теореме о трёх перпендикулярах BM [math]\perp[/math] MP. Следовательно, угол NMP — линейный угол искомого угла.

Длина NP равна половине высоты треугольника A₁B₁C₁, то есть [math]NP=\frac{3\sqrt3}2[/math]. Поэтому [math]\sin\angle NMP=\frac{NP}{MN}=\frac{3\sqrt3}{2\times3\sqrt2}=\frac{\sqrt3}{\sqrt8}[/math]

Следовательно, [math]\angle NMP=arc\sin\sqrt{\frac38}[/math]

Ответ: б) [math]\arcsin\sqrt{\frac38}[/math]