Задание № 30249
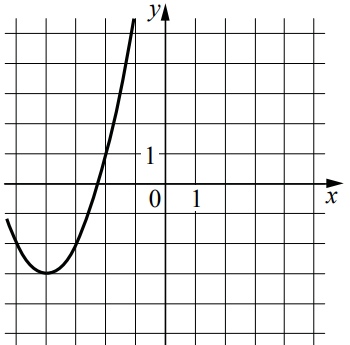
На рисунке изображён график функции вида [math]f\left(x\right)=ax^2+bx+c[/math] , где числа a , b и c — целые. Найдите значение [math]f\left(-12\right)[/math].
Решать другие задания по теме: Графики функций
Показать ответ
Комментарий:
По графику из задания видим, что у параболы коэффициент а = 1.
Вершина параболы находится в точке (-4; -3). Координата х вершины параболы находится по формуле:
[math]x=\frac{-b}{2a}[/math]Подставим значения и найдём b:
[math]-4=\frac{-b}{2a}{}\\-b=-4\cdot2{}\\b=8[/math]Подставив координаты вершины параболы х и у найдём коэффициент с:
[math]y=ax^2+bx+c{}\\-3=1\cdot(-4)^2+8\cdot(-4)+c{}\\-3=16-32+c{}\\c=13[/math]Функция имеет вид:
[math]f(x)=x^2+8x+13[/math]Найдём f(-12):
[math]f(-12)=\left(-12\right)^2+8\cdot(-12)+13=144-96+13=61[/math] Ответ:Нашли ошибку в задании? Выделите фрагмент и нажмите Ctrl + Enter.