Задание № 30240
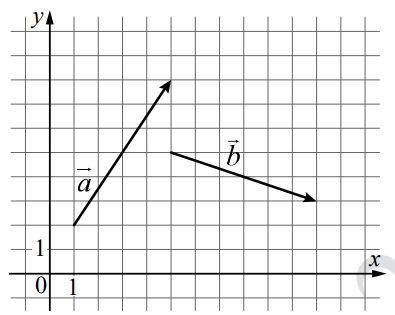
На координатной плоскости изображены векторы [math]\vec a\;и\;\vec b[/math]. Найдите скалярное произведение [math]\vec a\;\cdot\;\vec b[/math].
Решать другие задания по теме: Задания на векторы
Показать ответ
Комментарий:
Найдём координаты векторов, найдя на рисунке координаты точек начала и точек конца каждого вектора:
[math]\vec a[/math]{[math]x_2-x_1;y_2-y_1[/math]} = [math]\vec a[/math]{5 - 1; 8 - 2} = [math]\vec a[/math]{4;6}
[math]\vec b[/math] {[math]x_2-x_1;y_2-y_1[/math]} = [math]\vec b[/math] {11 - 5; 3 - 5} = [math]\vec b[/math] {6; -2}
Найдём скалярное произведение векторов:
[math]\vec a\cdot\vec b=x_1\cdot x_2+y_1\cdot y_2[/math] = 4 • 6 + 6 • ( -2) = 24 - 12 = 12
Ответ: 12Нашли ошибку в задании? Выделите фрагмент и нажмите Ctrl + Enter.