Имеем два случая: [math]x<0[/math],[math]x\geq0[/math]

1 случай: [math]x\geq0[/math]. Преобразуем функцию:

[math]f(x)=x^3-6x^2+(9+6a-3a^2)x[/math]

Найдем производную функции:

[math]f'(x)=3x^2-12x+(9+6a-3a^2)[/math]

[math]f'(x)=0[/math]

[math]x^2-4x+3+2a-a^2=0[/math]

[math]D=16-4(3+2a-a^2)=4(a-1)^2[/math]

[math]x_1=3-a[/math], [math]x_2=1+a[/math]

Определим знак производной:

1) 0<a<1; 1<a+1<2; 2<3-a<3

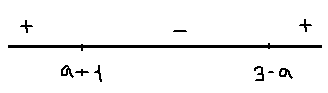
x=a+1- точка максимума;fmax=

[math]fmax=f(a+1)=-2(a+1)(a^2-a-2)[/math]

2) 1<a<2; 2<a+1<3;1<3-a<2

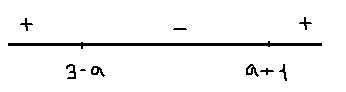
x=3-a-точка максимума

[math]fmax=f(3-a)=2(3-a)(6-a)[/math]

3)2<a<3; 3<a+1<4; 0<3-a<1

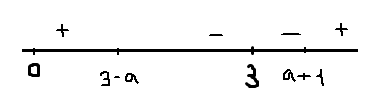
x=a+1 не принадлежит отрезку x=3-a- точка максимума

4)a>3

x=a+1,x=3-a не принадлежат отрезку значений x

т.к. функция убывает, то fmax=f(0)=0

2 случай: x<0. Преобразуем функцию:

[math]f(x)=-x^3-6x^2+(-9+6a+3a^2)x[/math]

Найдем производную функции:

[math]f'(x)=-3x^2-12x+(-9+6a+3a^2)[/math]

[math]f'(x)=0[/math]

[math]x^2+4x+3-2a-a^2=0[/math]

[math]D=16-4(3-2a-a^2)=4(a+1)^2[/math]

[math]x_1=-3-a[/math], [math]x_2=-1+a[/math]

Определим знак производной:

1) -1<a<0;-3<-3-a<-2; -2<a-1<-1

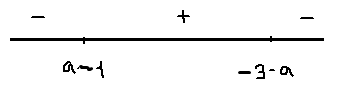
x=a-1- точка максимума;fmax=

[math]fmax=f(a-1)=-2(a-1)(a^2+2a+2)[/math]

2) -2<a<-1; -3<a-1<-2;-2<-3-a<-1

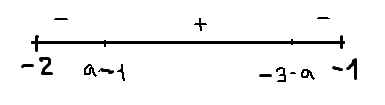
x=-3-a-точка максимума

[math]fmax=f(-3-a)=2a(-3-a)(a+3)[/math]

3)-3<a<-2; -4<a1<-3;

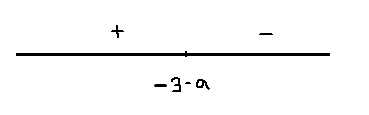
x=-3-a точка максимума

[math]fmax=f(-3-a)=2a(-3-a)(a+3)[/math]

4)a<-3; a-10

т.к. функция убывает, то [math]fmax=f(-3)=-9a^2-18a[/math]

Ответ:

при a≤-3 f_max=–9a2–18a;

при -3<a≤-1 f_max=-2a(a+3)²;

при -1<a≤0 f_max=2·(a–1)·(a2+2a+2);

при 0<a≤1 f_max=(a+1)·(–2a2+2a+4));

при 1<a≤3 f_max=2·(3–a)·(6–a);

при a>3 f_max=0.