Вариант 15

Для объектов, указанных в таблице, определите, какими числами они обозначены на плане. Заполните таблицу. В ответе запишите последовательность четырёх чисел без пробелов и других дополнительных символов.

Тротуарная плитка продаётся в упаковках по 8 штук. Какое наименьшее число упаковок плитки понадобилось купить, чтобы выложить ими все дорожки и площадки, отмеченные на плане?

Найдите площадь бассейна (в м²).

Найдите кратчайшее расстояние (в м) от жилого дома до бани.

У хозяина есть выбор при определении водоснабжения: скважина или водопровод. Стоимость изготовления скважины или водопровода, стоимость монтажных работ и необходимых материалов для этого, а также реальная стоимость воды при эксплуатации скважины или водопровода приведены в таблице.

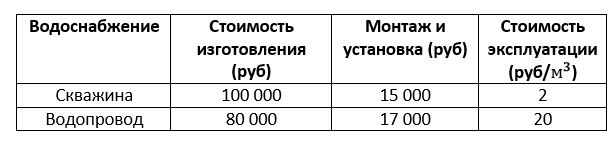
Обдумав оба варианта, хозяин решил изготавливать скважину.

Через сколько месяцев работы скважины будет компенсирована разность между стоимостью изготовления, монтажа и материалов, эксплуатации скважины и стоимостью изготовления, монтажа и материалов, эксплуатации водопровода?

Найдите значение выражения [math](\frac{17}{16}-\frac1{32})\div\frac{11}{24}[/math]

На координатной прямой отмечены числа x и y . Какое из приведённых ниже утверждений для этих чисел неверно?

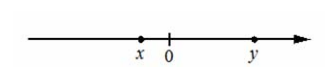
1) [math]у-х<0[/math]

2) [math]х^2у>0[/math]

3) [math]ху<0[/math]

4) [math]х+у>0[/math]

Найдите значения выражения [math]5\times10^2+4\times10^0+3\times10^{-1}+7\times10^{-2}+8\times10^{-4}[/math]

Решите уравнение [math]4-\frac х7=\frac х9[/math]. Если корней несколько, запишите их в ответ без пробелов и других дополнительных символов в порядке возрастания.

Гена, Юра, Филипп, Вадим и Таня бросили жребий – кому начинать игру. Найдите вероятность того, что начинать игру должна будет Таня.

Установите соответствие между графиками функций и функциями, которые задают эти графики. В ответе запишите три цифры, соответствующие буквам А, Б, В, без пробелов и других дополнительных символов.

А)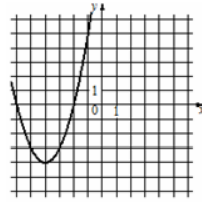

Б)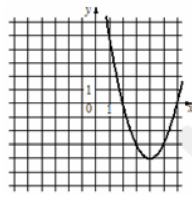

В)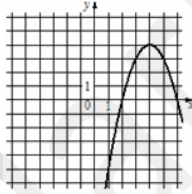

1) [math]у=х^2+8х+12[/math]

2) [math]у=х^2-8х+12[/math]

3) [math]у=-х^2+8х-12[/math]

В геометрической прогрессии сумма первого и второго членов равна 75, а сумма второго и третьего членов равна 150. Найдите первые три члена этой прогрессии. В ответе запишите первый, второй и третий члены прогрессии без пробелов и других дополнительных символов.

Найдите значение выражения [math]\frac{8ab}{a+8b}\times(\frac a{8b}-\frac{8b}a),\;если\;a=8\sqrt5+6\;,\;b=\sqrt5-3[/math]

Зная длину своего шага, человек может приближённо подсчитать пройденное им расстояние s по формуле [math]s=n\times l[/math], где n число шагов, l – длина шага. Какое расстояние прошёл человек, если l = 50 см, n = 1100 ? Ответ дайте в километрах.

Укажите норме решения неравенства [math]8х-х^2\leq0[/math]

1) [math]\lbrack0;\;+\infty)[/math]

2) [math](-\infty;\;0\rbrack\cup\lbrack8;\;+\infty)[/math]

3) [math]\lbrack8;\;+\infty)[/math]

4) [math]\lbrack0;\;8\rbrack[/math]

Один из острых углов прямоугольного треугольника равен [math]53^\circ[/math]. Найдите градусную меру другого острого угла.

Из точки A проведены две касательные к окружности с центром в точке O. Найдите расстояние от точки A до точки O , если угол между касательными равен [math]60^\circ[/math] , а радиус окружности равен 8.

Основания трапеции равны 20 и 26, одна из боковых сторон равна [math]8\sqrt3[/math] , а угол между ней и одним из оснований равен [math]120^\circ[/math] . Найдите площадь трапеции.

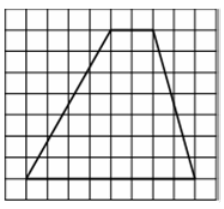
На клетчатой бумаге с размером клетки 1 × 1 изображена трапеция. Найдите длину её средней линии.

Какие из следующих утверждений верны? Запишите их номера без пробелов и других дополнительных символов в порядке возрастания.

1) Вокруг любого треугольника можно описать окружность.

2) Если при пересечении двух прямых третьей прямой сумма внутренних односторонних углов равна [math]180^\circ[/math] , то эти прямые параллельны.

3) Площадь треугольника не превышает произведения двух его сторон.

Решите системы неравенств

[math]\frac{3-х}{1+(5-х)^2}\geq0[/math]

[math]8-7х\leq24-3х[/math]

Теплоход проходит по течению реки до пункта назначения 280 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 4 км/ч, стоянка длится 15 часов, а в пункт отправления теплоход возвращается через 39 часов после отправления из него.

Постройте график функции [math]у=-4-\frac{х+1}{х^2+х}[/math] . Определите, при каких значениях прямая m не имеет с графиком функции y=m общих точек.

Биссектрисы углов A и D параллелограмма ABCD пересекаются в точке, лежащей на стороне BC . Найдите BC , если AB = 42 .

В параллелограмме KLMN точка E – середина стороны KN . Известно, что EL = EM . Докажите, что данный параллелограмм –прямоугольник.

На стороне BC остроугольного треугольника ABC ( AB ≠ AC) как на диаметре построена полуокружность, пересекающая высоту AD в точке M . Известно, что AD = 80 , MD = 64 . Найдите AH , где H – точка пересечения высот треугольника ABC .