Вариант 12
Часть 1.
Ответами к заданиям 1–20 являются число или последовательность цифр, которые следует записать в поле соответствующего задания. Если ответом является последовательность цифр, то запишите её без пробелов, запятых и других дополнительных символов.
Прочитайте внимательно текст и выполните задания 1–5
На плане (см. рисунок) изображена вертолётная взлётно‐посадочная площадка, которую требуется построить. Сначала будет строиться квадратная площадка размером 20 м × 20 м, а затем к ней будут пристраиваться 4 одинаковые прямоугольные площадки 20 м × 14 м так, как показано на плане. Точками A1 , A2 , …, A12 отмечается внешний периметр площадки.
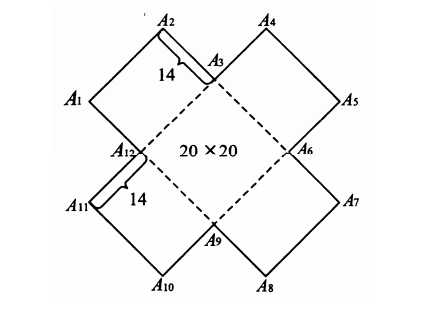
Заказчик планирует покрыть всю площадку специальным материалом одной из двух фирм: «Ореол» или «Оптимист».
В нижней строке таблицы укажите нижний индекс точек, симметричных соответствующим точкам, указанным в верхней строке таблицы, относительно центра симметрии площадки. Заполните таблицу. В ответе запишите последовательность четырёх цифр без пробелов и других дополнительных символов.

Планируется для 1м2 площадки использовать 4 кг покрытия. Какое наименьшее число банок покрытия понадобится для всей площадки, если оно будет приобретаться банками по 15 кг?
Найдите периметр (в м) вертолётной площадки.
Найдите наибольшее расстояние (в метрах) между произвольными точками внешнего периметра площадки.
Стоимость покрытия, стоимость работ по его нанесению и расходы на эксплуатацию указаны в таблице.

Заказчик решил закупить покрытие у фирмы «Ореол». Через сколько лет экономия от уменьшения стоимости эксплуатации этого покрытия компенсирует разность в стоимости покрытия и его нанесения по сравнению с вариантом от фирмы «Оптимист»?
Найдите значение выражения [math]0,6\times(-10)^4+4\times(-10)^3+70[/math]
Известно, что a>b>0. Какое из указанных утверждений верно?
1) 2а+1 < 0
2) -a > -b
3) 2b > 2a
4) 1-a < 1-b
Найдите значение выражения [math]7\sqrt2\times3\sqrt5\times2\sqrt{10}[/math]
Решите уравнение [math]x^2-5x=14[/math] . Если корней несколько, запишите их в ответ без пробелов и других дополнительных символов в порядке возрастания.
Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд будет первой владеть мячом. Команда A должна сыграть два матча с командой B и с командой C. Найдите вероятность того, что в обоих матчах первой мячом будет владеть команда A .
Установите соответствие между графиками функций вида [math]y=\frac kx[/math] и функциями, которые задают эти графики. В ответе запишите три цифры, соответствующие буквам А, Б, В, без пробелов и других дополнительных символов.
А) 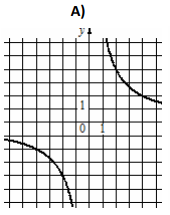
Б) 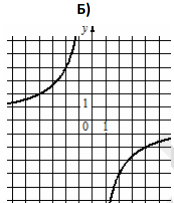
В) 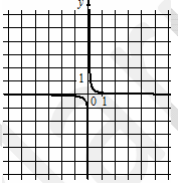
1) [math]у=\frac8х[/math] 2) [math]у=\frac1{8х}[/math] 3) [math]у=-\frac8х[/math]
Выписаны первые три члена геометрической прогрессии: -196; 392; -784. Найдите её пятый член.
Найдите значение выражения [math](\frac{m-n}{m^2+mn}+\frac1m)\div\frac m{m+n}[/math] , если m= -0,25 и n=[math]\sqrt5-1[/math]
Мощность постоянного тока (в Вт) можно вычислить по формуле [math]P=I^2R[/math] , где I – сила тока (в А), R – электрическое сопротивление (в Ом). Пользуясь этой формулой, найдите сопротивление R (в Ом), если мощность составляет 150 Вт, а сила тока равна 5 А.
Укажите номер решения неравенства 3х–2(х–2) > –4
1) [math](0;\;+\infty)[/math]
2) [math](-8;\;+\infty)[/math]
3) [math](-\infty;\;0)[/math]
4) [math](-\infty;\;-8)[/math]
Площадь прямоугольного треугольника равна [math]\frac{1058}{\sqrt3}[/math] . Один из углов равен [math]30^\circ[/math] . Найдите длину катета, лежащего напротив этого угла.
Найдите градусную меру угла АСН правильного восьмиугольника ABCDEFGH.
В трапеции ABCD известно, что AD = 6 , BC = 1, а её площадь равна 84. Найдите площадь треугольника ABC .
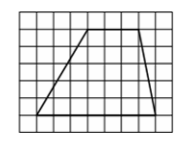
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.
Какие из следующих утверждений верны? Запишите их номера без пробелов и других дополнительных символов в порядке возрастания.
1) Если противоположные углы выпуклого четырёхугольника попарно равны, то этот четырёхугольник – параллелограмм.
2) Сумма двух противоположных углов четырёхугольника не превосходит 180 градусов
3) Если основания трапеции равны 4 и 6, то средняя линия равна 10
Часть 2.
При выполнении заданий 21–26 используйте тетрадь. Сначала укажите номер задания, а затем запишите его решение и ответ. Пишите чётко и разборчиво.
Решите систему уравнений
[math]4х^2-5х=у{}\\8х-10=у[/math]
Три бригады вместе изготовили 114 синхронизаторов передач. Известно, что вторая бригада изготовила синхронизаторов в 3 раза больше, чем первая, и на 16 синхронизаторов меньше, чем третья. На сколько синхронизаторов передач больше изготовила третья бригада, чем первая?
Постройте график функции [math]y=\frac{\left(\sqrt{x^2+3x}\right)^2}x[/math] . Определите, при каких значениях m прямая y=m не имеет с графиком функции общих точек.
Стороны AC , AB , BC треугольника ABC равны [math]2\sqrt2[/math] , [math]\sqrt5[/math] и 1 соответственно. Точка K расположена вне треугольника ABC , причём отрезок KC пересекает отрезок AB в точке, отличной от B . Известно, что треугольник с вершинами K, A, C подобен треугольнику ABC . Найдите градусную меру угла AKC , если [math]\angle KAC>90^\circ[/math]
В окружности через середину O хорды BD проведена хорда AC так, что дуги AB и CD равны. Докажите, что O – середина хорды AC .
Точки M и N лежат на стороне AC треугольника ABC , причём AM = 36 и AN = 44 . Найдите радиус окружности, проходящей через точки M и N и касающейся луча AB , если [math]\cos\left(\angle BAC\right)=\frac{\sqrt{11}}6[/math]
| № | Ваш ответ | Ответ и решение | Первичный балл |
|---|---|---|---|
|
Здесь появится результат первой части. Нажмите на кнопку «Завершить работу», чтобы увидеть правильные ответы и посмотреть решения. |
|||