Вариант 11
Часть 1.
Ответами к заданиям 1–20 являются число или последовательность цифр, которые следует записать в поле соответствующего задания. Если ответом является последовательность цифр, то запишите её без пробелов, запятых и других дополнительных символов.
Прочитайте внимательно текст и выполните задания 1–5
На плане (см. рисунок) изображена усадьба Петра Михайловича.
Усадьба имеет форму прямоугольника (сторона каждой клетки равна 2 метрам).
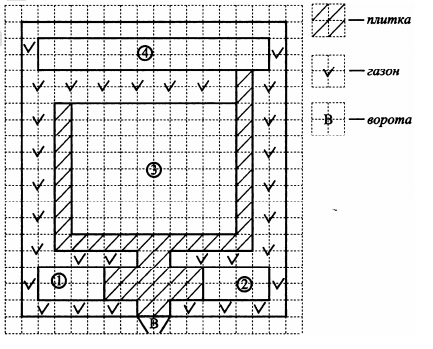
Въезд и выезд осуществляются через единственные ворота. Усадьба огорожена с четырёх сторон кирпичным забором длиной 132 метра (не считая ворот).
При входе в усадьбу слева от ворот находится гараж. Справа расположена баня, площадь которой равна 32 кв. м. Жилой дом находится в центре усадьбы. Вокруг дома посажена трава, а за домом имеются хозяйственные постройки.
Дорожки внутри участка и площадка между баней и гаражом вымощена тротуарной плиткой размером 1 м × 1 м.
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу. В ответе запишите последовательность четырёх цифр без пробелов и других дополнительных символов.

Тротуарная плитка продаётся в упаковках по 5 штук. Сколько упаковок плитки понадобилось купить, чтобы выложить все дорожки и площадки усадьбы?
Найдите площадь земли (в м2), которую занимают жилой дом.
Найдите расстояние (в метрах) от гаража до бани (расстояние между двумя ближайшими точками).
Пётр Михайлович планировал построить забор вокруг участка. Он рассмотрел два варианта: сделать кирпичный забор или каменный.
Цены на фундамент (за погонный метр) и его укладку, стоимость кирпича и камня даны в таблице.

Обдумав оба варианта, Пётр Михайлович решил построить кирпичный забор.
Определите, на сколько рублей выгоднее построить кирпичный забор, чем каменный.
Найдите значение выражения
[math](\frac3{22}+\frac2{11})\div\frac5{33}[/math]Известно, что [math]-1<а<0[/math] . Какое из чисел [math]а^3,\;а^4,а^5[/math] наименьшее
1) [math]а^3[/math]
2) [math]а^4[/math]
3) [math]а^5[/math]
4) невозможно определить
Найдите значение выражения [math]\frac{5^{-2-n}}{5^{-1-n}}[/math]
Решите уравнение 9+10(3х-10)=2 . Если корней несколько, запишите их в ответ без пробелов и других дополнительных символов в порядке возрастания.
Из 500 мониторов, поступивших в продажу, в среднем 15 не работают. Какова вероятность того, что случайно выбранный монитор работает?
Установите соответствие между графиками функций вида [math]y=ax^2+bx+c[/math] и функциями, которые задают эти графики. В ответе запишите три цифры, соответствующие буквам А, Б, В, без пробелов и других дополнительных символов.
А)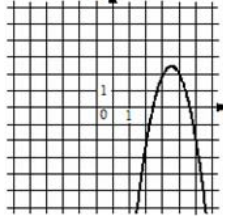
Б) 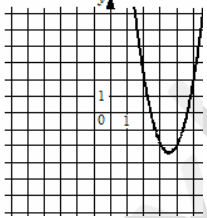
В) 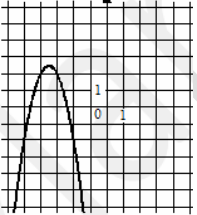
1) [math]y=2x^2-14x+22[/math]
2) [math]y=-2x^2-14x-22[/math]
3) [math]y=-2x^2+14x-22[/math]
Геометрическая прогрессия задана условием [math]b_n=62,5\times2^n[/math]. Найдите сумму первых четырёх её членов.
Найдите значение выражения [math]\frac{16x-25y}{4\sqrt x-5\sqrt y}-\sqrt y[/math] если [math]\sqrt x+\sqrt y=3[/math] и [math]4\sqrt x-5\sqrt y\neq0[/math]
Площадь трапеции (в м2) можно вычислить по формуле S=[math]\frac12(a+b)h[/math], где a и b – основания трапеции (в метрах), h – высота (в метрах). Пользуясь этой формулой, найдите высоту , если основания трапеции равны 5 м и 7 м, а её площадь равна 24 м 2
При каких значениях x значение выражения 9x+7 меньше значения выражения 8х-3 ?
1) (4; +[math]\infty[/math])
2) (-[math]\infty[/math]; 4)
3) (-10; +[math]\infty[/math])
4) (-[math]\infty[/math]; -10)
В остроугольном треугольнике ABC высота AH равна 20√3 , а сторона AB равна 40. Найдите cos∠ABC
На отрезке AB выбрана точка С так, что AC = 21 и BC = 8, Построена окружность с центром в точке А, проходящая через точку С. Найдите длину отрезка касательной, проведённой из точки В к этой окружности.
Высота ВН ромба ABCD делит его сторону AD на отрезки АН=48 и HD=25. Найдите площадь ромба.
Из квадрата с диагональю [math]5\sqrt2[/math] вырезали прямоугольник со сторонами 3 и 4. Найдите площадь получившейся фигуры.
Какие из следующих утверждений верны? Запишите их номера без пробелов и других дополнительных символов в порядке возрастания.
1) В любую равнобедренную трапецию можно вписать окружность.
2) Диагональ параллелограмма делит его углы пополам.
3) Площадь прямоугольного треугольника равна половине произведения его катетов
Часть 2.
При выполнении заданий 21–26 используйте тетрадь. Сначала укажите номер задания, а затем запишите его решение и ответ. Пишите чётко и разборчиво.
Решите уравнение [math]х^3+3х^2-х-3=0[/math]
[math]х^3+3х^2-х-3=0[/math]
x2(x+3)-(x+3)=0
(x2-1)(x+3)=0
x2-1=0 или x+3=0
x1=-1, x2=1, x31=-3
Ответ: -3;-1;1
Первые два часа автомобиль ехал со скоростью 65 км/ч, следующие 4 часа – со скоростью 105 км/ч, а последние 4 часа – со скоростью 80 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
[math]v_{ср}=\frac{S_{весь}}{t_{все}}=\frac{2\cdot65+4\cdot105+4\cdot80}{2+4+4}=\frac{870}{10}=87[/math] км/ч
Ответ: 87
Постройте график функции [math]у=\frac{(х^2+6,25)(х+1)}{-1-х}[/math]. Определите, при каких значениях р прямая у=рх имеет с графиком функции ровно одну общую точку.
ОДЗ: x≠-1
Упростим функцию
[math]у=\frac{(х^2+6,25)(х+1)}{-1-х}[/math]
y=-x2-6,25 , при x≠-1
Парабола типа y=x2, ветви вниз, вершина (0;-6,25), без растяжений и сжатий.
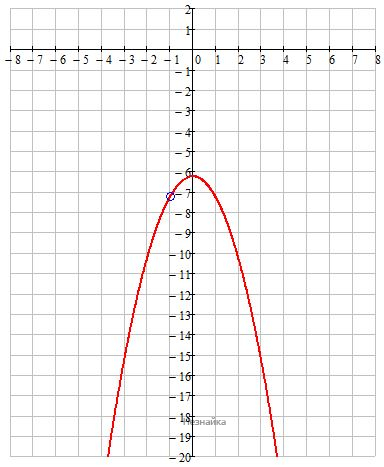
Определим, при каких значениях р прямая у=рх имеет с графиком функции ровно одну общую точку.
у=рх=-x2-6,25
рх=-x2-6,25
x2+рх+6,25=0
Уравнение имеет ровно один корень, а соответственно и прямая с графиком ровно одну общую точку, когда D=0
D=р2-4•6,25=р2-25=0
p1,2=±5
Рассмотрим вариант, когда x=-1
[math]x_{1,2}=\frac{-p\pm\sqrt{p^2-25}}2=-1[/math]
±√(р2-25)=-2+p
1) √(p2-25)=-2+p
при -2+p>0→p>2
p2-25=(-2+p)2
p2-25=p2-4p+4
-25=-4p+4
4p=29
p=7,25 >2
2) -√(p2-25)=-2+p
√(p2-25)=2-p
при 2-p>0→p<2
p2-25=(2-p)2
p2-25=4-4p+p2
-25=4-4p
4p=29
p=7,25 - не удовлетворяет условию p<2
Таким образом при p∈{-5;5;7,25} прямая у=рх имеет с графиком функции ровно одну общую точку.
Ответ: {-5;5;7,25}
Прямая AD перпендикулярная медиане ВМ треугольника АВС, делит медиану ВМ пополам. Найдите сторону АС, если сторона АВ равна 4.
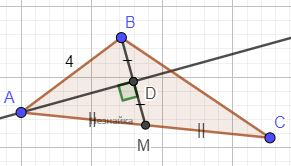
Прямоугольные треугольники ABD и AMD равны между собой по двум катетам: BD=MD, AD - общая. Следовательно AB=AM=4.
Так как BM - медиана, то AM=MC=4
AC=AM+MC=4+4=8
Ответ: 8
В параллелограмме ABCD точка М — середина стороны CD. Известно, что МА=МВ. Докажите, что данный параллелограмм — прямоугольник.
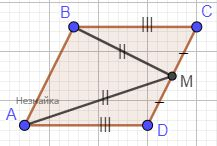
В параллелограмме противоположные стороны равны, т.е. AD=BC. Так как М — середина стороны CD, то CM=MD. Известно, что МА=МВ.
Таким образом треугольники ADM и BCM равны между собой. Значит ∠ADM=∠BCM.
В параллелограмме сумма смежных углов равна 180°, т.е. ∠ADM+∠BCM=180°
∠ADM+∠ADM=180° → ∠ADM=∠BCM=90°
Таким образом параллелограмм, является прямоугольником, так как его угол равен 90°
Три окружности с центрами [math]О_1[/math] , [math]О_2[/math] , [math]О_3[/math] и радиусами 6, 1, 7 соответственно попарно касаются внешним образом. Найдите градусную меру угла [math]О_1О_2О_3[/math]
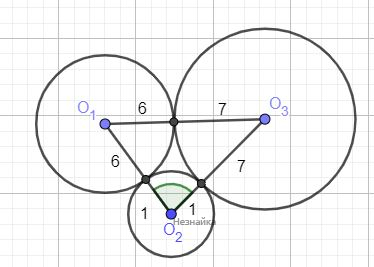
По теореме косинуса:
[math]cos(\angle O_1O_2O_3)=\frac{O_1O_2^2+O_2O_3^2-O_1O_3^2}{2\cdot O_1O_2\cdot O_2O_3}=[/math]
[math]=\frac{7^2+8^2-13^2}{2\cdot7\cdot8}=[/math]
[math]=-\frac{56}{112}=-\frac12[/math]
∠O1O2O3=arccos(-0,5)=120°
Ответ: 120°
| № | Ваш ответ | Ответ и решение | Первичный балл |
|---|---|---|---|
|
Здесь появится результат первой части. Нажмите на кнопку «Завершить работу», чтобы увидеть правильные ответы и посмотреть решения. |
|||