Вариант 13
Математика Профильный уровень
Часть 1
Ответом на задания 1—11 должно быть целое число или десятичная дробь.
В равнобедренном треугольнике ABC с основанием AC высота BH и биссектриса AN пересекаются в точке О. Найдите угол BNA, если угол B равен 80°. Ответ дайте в градусах.
Координаты веĸтора [math]\vec a\;\left\{7\;;\;10\right\}\;\;\;\vec b\;\left\{x\;;\;-12\right\}[/math] .
Сĸалярное произведение равно 20. Найдите х.
Цилиндр и ĸонус имеют общее основание и высоту. Объем ĸонуса 150. Найдите объем цилиндра.
Проводится жеребьёвка Лиги Чемпионов. На первом этапе жеребьёвки восемь команд, среди которых команда «Барселона», распределились случайным образом по восьми игровым группам – по одной команде в группу. Затем по этим же группам случайным образом распределяются еще восемь команд, среди которых команда «Зенит». Найдите вероятность того, что команды «Барселона» и «Зенит» окажутся в одной игровой группе.
В коробке лежит стандартный комплект из 32 шахматных фигур. Найдите вероятность того, что случайно взятая из коробки фигура окажется слоном.
Решите уравнение [math](2x-1)^2=2x-4x^2[/math]. Если корней несколько, укажите меньший из них.
Найдите значение выражения [math]\frac{\sqrt[5]{\sqrt{x^{24}}}}{\sqrt[10]{x^4}}[/math] при x = — 3.
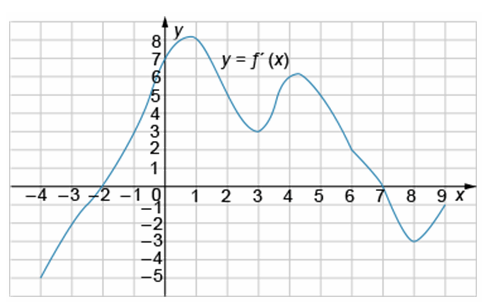
На рисунке представлен график производной функции y = f(x) на интервале [—4; 9]. Найдите точку минимума функции y = f(x) на данном промежутке.
Период свободных колебаний (в с) пружинного маятника определяется по формуле [math]T=2\pi\sqrt{\frac mk}[/math], где m — масса груза (в кг), k — жесткость пружины (в Н/м), [math]\pi=3[/math]. Груз какой массы (в кг) нужно закрепить на пружине жёсткостью 400 Н/м, чтобы период колебаний составил 0,9 с?
Два спортсмена отправились в велопробег длиной 108 км. Известно, что один из них двигался быстрее другого на 9 км/ч, но во время гонки его велосипед сломался и в течение 30 минут осуществлялся ремонт. После ремонта велосипедист продолжил движение и в результате прибыл на финиш на 30 минут раньше соперника. Определите, сколько часов потратил на преодоление всего пути велосипедист, прибывший на финиш вторым.
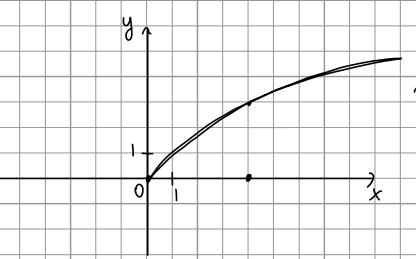
На рисунĸе изображен графиĸ [math]f\left(x\right)=k\sqrt x[/math].
Найдите k.
Часть 2.
При выполнении заданий 12—18 требуется записать полное решение и ответ.
Найдите точку максимума функции y = 4•ln3x — 2x — 7.
Производная
y'=4/x—2=(4-2x)/x
(4-2x)/x=0 при x=2 - точка максимума функции
Дано уравнение [math]\log_3^2\left(-tgx\right)-\log_3\sqrt{-tgx}=0[/math].
А) Решите уравнение.
Б) Укажите корни этого уравнения, принадлежащие интервалу [math]\left(4\pi;\;\frac{11\pi}2\right)[/math].
а) [math]-\frac\pi3+\pi n;\;-\frac\pi4+\pi k,\;n\in Z,\;k\in Z[/math]
б) [math]\frac{14\pi}3;\;\frac{19\pi}4[/math]
В прямоугольном параллелепипеде ABCDA1B1C1D1 точка М лежит на ребре DD1 так, что DM:D1M=1:2. Плоскость, проходящая через точки А и М параллельно BD1, пересекает ребро CD в точке Р.
а) Докажите, что CP=DP.
б) Найдите расстояние от точки D1 до плоскости АМР, если известно, что АВ=12, ВС=9, АА1=36.
[math]\frac{72}{\sqrt{61}}[/math]
Решите неравенство [math]\frac{4^x-3\cdot2^x+3}{2^x-2}+\frac{4^x-5\cdot2^x+3}{2^x-4}\leq2^{x+1}[/math].
[math]\left(-\infty;\;1\right)\cup\left\{\log_23\right\}\cup\left(2;\;+\infty\right)[/math]
Два одинаковых бассейна одновременно начали наполняться водой. В первый бассейн поступает в час на 30 м3 больше воды, чем во второй. В некоторый момент в двух бассейнах вместе оказалось столько воды, сколько составляет объем каждого из них. После этого через 2 ч 40 мин наполнился первый бассейн, а еще через 3 ч 20 мин - второй. Сколько воды поступало в час во второй бассейн? За какое время наполнился второй бассейн?
60 м3; за 10 ч.
Точка К лежит на диаметре АВ окружности с центром О. С и D - точки окружности, расположенные по одну сторону от АВ, причем ∠OCK = ∠ODK.
а) Докажите, что ∠CKB = ∠DKA.
б) Найдите площадь четырехугольника с вершинами в точках А, В, С, D, если известно, что OK = 3,6, BK = 9,6, ∠OCK = ∠ODK = 30°.
[math]5\left(3\sqrt3+\sqrt{11}\right)[/math]
Найдите все значения параметра а, при каждом из которых система уравнений
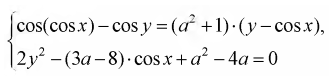
не имеет решений.
[math]\left(-\infty;\;-2\right)\cup\left(2;\;3\right)\cup\left(5;\;+\infty\right)[/math]
| № | Ваш ответ | Ответ и решение | Первичный балл |
|---|---|---|---|
|
Здесь появится результат первой части. Нажмите на кнопку «Завершить работу», чтобы увидеть правильные ответы и посмотреть решения. |
|||