Вариант 4
Математика Профильный уровень
Часть 1
Ответом на задания 1—11 должно быть целое число или десятичная дробь.
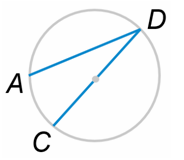
В окружности проведен диаметр DC и хорда AD. Угол ADC равен 15°. Найдите угол ACD (в градусах).
Найдите длину веĸтора [math]\vec{AB}\;\left\{7\;;\;24\right\}[/math]
Во сĸольĸо раз увеличится объем ĸонуса если радиус его основания увеличится в 5 раз, а высота в 2 раза
Магазин проводит лотерею среди покупателей. На 100 билетов приходится 16 единиц бытовой техники, 25 предметов посуды, все остальные призы — сувениры с символикой. Какова вероятность того, что случайно зашедшему в этот день посетителю достанется сувенир?
Механические часы с двенадцатичасовым циферблатом в какой-то момент остановились. Найдите вероятность того, что часовая стрелка остановилась, достигнув отметки , но не дойдя до отметки .
Решите уравнение [math]7^{5x^2-20}=7^{15x}[/math]. В ответе укажите бо́льший его корень.
Вычислите [math]\frac{sin^2765^\circ}{1-cos420^\circ}[/math]
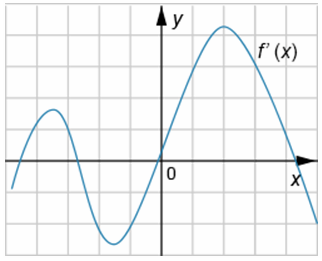
На рисунке изображен график производной функции f(x). Определите количество целых точек, в которых касательная к графику f(x) будет иметь тангенс угла наклона, равный 1.
Для выполнения трюка мотоциклист движется по внутренней поверхности цилиндра по окружности, перпендикулярной оси цилиндра. Необходимая минимальная скорость для движения по данной траектории вычисляется по формуле: [math]v_{min}=\sqrt{g\left(r-l\right)\mu}[/math]. Определите, при каком коэффициенте трения покрышек μ о поверхность цилиндра скорость мотоцикла будет равна [math]v_{min}=7,8[/math] м/с. Радиус цилиндра r = 11 м, расстояние от центра тяжести мотоцикла с человеком до поверхности цилиндра l = 0,86 м, ускорение свободного падения принять равным g = 10 м/c2.
Для освещения магазина необходимо установить 286 светильников. Рабочие в первый день установили 10 шт. За сколько дней работа будет выполнена, если каждый следующий день они устанавливали на 2 светильника больше?
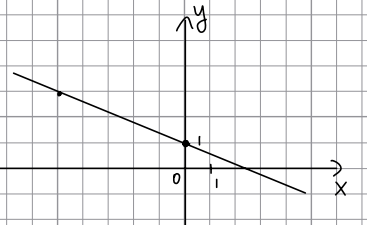
На рисунĸе изображен графиĸ [math]f\left(x\right)=kx+b[/math].
Найдите b
Часть 2.
При выполнении заданий 12—18 требуется записать полное решение и ответ.
Найдите точку минимума функции [math]f(x)=-12ln(x^2-12)+6x[/math].
Область определения функции: [math]x\in(-\infty;-\sqrt{12})\cup(\sqrt{12};\infty)[/math]
Найдем производную и определим точки экстремума
[math]f'(x)=-12\cdot\\frac{2x}{x^2-12}+6[/math]
При f'(x)=0
[math]-12\cdot\\frac{2x}{x^2-12}+6=0[/math]
[math]x^2-4x-12=0[/math]
[math]D=4^2-4\cdot1\cdot\left(-12\right)=64[/math]
[math]x_1=\\frac{4-\sqrt{64}}2=-2[/math]
[math]x_2=\\frac{4+\sqrt{64}}2=6[/math]
При x<-√12 производная положительная — функция возрастает, при √12<x<6 производная отрицательная — функция убывает, при х>6 производная положительная — функция возрастает
Точка минимума: x=6
Дано уравнение [math]\frac{\sin x+\sin3x}{\cos x}=1[/math].
А) Решите уравнение.
Б) Укажите корни этого уравнения, принадлежащие отрезку [math]\left[\frac14;\;\frac{13}4\right][/math].
А) Преобразуем левую часть уравнения и получим следующее:
[math]\frac{2sin(2x)cosx}{cosx}=1[/math]
ОДЗ: [math]cosx\neq0[/math] , [math]x\neq\frac\pi2+\pi n,n\in Z[/math]
[math]2sin2x=1[/math]
[math]sin2x=\frac12[/math]
[math]x_1=\frac\pi{12}+\pi k,\;k\in Z[/math]
[math]x_2=\frac{5\pi}{12}+\pi n,\;n\in Z[/math]
Б) Нанесем корни на числовую прямую и определим, какие из них войдут в отрезок
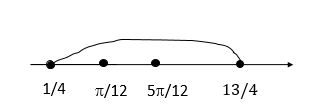
Ответ: А) [math]\frac\pi{12}+\pi k,\;\frac{5\pi}{12}+\pi n,\;k,n\in Z;[/math]
Б) [math]\frac\pi{12};\;\frac{5\pi}{12}[/math]
В правильной треугольной призме АВСА1B1C1 все ребра равны между собой. Точка К - середина ребра СС1.
А) Докажите, что прямые АВ1 и ВК перпендикулярны.
Б) Найдите расстояние между прямыми АВ1 и ВК, если ребро призмы равно 6.
Решение:
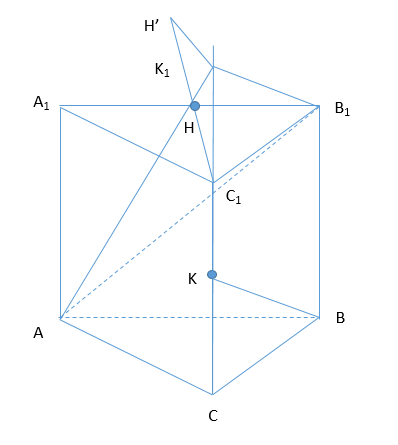
Все ребра равны, правильная призма, [math]C_1K=CK[/math]
А) Доказать, что [math]AB_1\perp KB[/math]
Совершим параллельный перенос прямой КВ так, чтобы она проходила через точку [math]B_1[/math], пересекает [math]С_1С[/math] в т. [math]К_1[/math]
[math]\bigtriangleup СВК=\bigtriangleup С_1В_1К_1[/math] (по катет и острому углу):
[math]С_1В_1=СВ[/math], [math]\angle С_1В_1К_1=\angle СВК\Rightarrow К_1С_1=КС[/math]
Имеем, что [math]\angle(АВ_1;КВ)=\angle(АВ_1;К_1В_1)[/math]
Пусть а - длина ребра
Из [math]\bigtriangleup С_1К_1В_1[/math], [math]\angle С_1=90^\circ[/math], по теореме Пифагора : [math]К_1В_1=\sqrt{а^2+\frac{а^2}4}=\frac{а\sqrt5}2[/math]
Из [math]\bigtriangleup АК_1С_1[/math], [math]\angle С=90^\circ[/math], по теореме Пифагора : [math]АК_1=\sqrt{а^2+\frac{9а^2}4}=\frac{а\sqrt13}2[/math]
Из [math]\bigtriangleup АК_1С_1[/math]: [math]\angle В=90^\circ[/math] по теореме Пифагора: [math]АВ_1=\sqrt{а^2+а^2}=а\sqrt2[/math]
Проверим, является ли [math]\bigtriangleup АК_1В_1[/math] прямоугольным по теореме, обратной теореме Пифагора
[math]АК_1^2=АВ_1^2+К_1В_1^2[/math]
[math]\frac{а^2\cdot13}4=а^2\cdot2+\frac{а^2\cdot5}4[/math] - верно
Следовательно,[math]\bigtriangleup АВ_1К_1=90^\circ\Rightarrow\angle(АВ_1;К_1В_1)=\angle(АВ_1;КВ)\Rightarrow АВ_1\perp КВ[/math]
Б) Построим [math]С_1Н\perp А_1В_1[/math], [math]К_1H'\perp(AA_1B_1)[/math]
[math]C_1H\parallel K_1H'[/math] , [math]C_1K_1\parallel HH'\Rightarrow C_1H=K_1H'[/math]
Рассмотрим [math]\bigtriangleup С_1В_1H[/math] [math]\angle H=90^\circ[/math], [math]C_1H=\sqrt{C_1B_1^2-HB_1^2}[/math], по теореме Пифагора [math]HB_1=\frac12a[/math] ( по свойству равнобедренного треугольника)
[math]С_1Н=\sqrt{а^2-\frac{а^2}4}=\frac{а\sqrt3}2=К_1Н'[/math]
Рассмотрим пирамиду [math]K_1B_1BA[/math]:
С одной стороны [math]V_п=\frac13К_1Н'[/math] * [math]S_{\bigtriangleup ABB_1}[/math]
С другой стороны [math]V_п=\frac13h[/math] * [math]S_{\bigtriangleup AK_1B_1}[/math]
[math]\frac13К_1Н'[/math] * [math]S_{\bigtriangleup ABB_1}[/math] = [math]\frac13h\ast S_{\bigtriangleup AK_1B_1}\Rightarrow h=\frac{K_1H'\ast S_{\bigtriangleup ABB_1}}{S_{\bigtriangleup AK_1B_1}}[/math]
[math]S_{\bigtriangleup ABB_1}=\frac12a^2[/math], [math]S_{\bigtriangleup AK_1B_1}=\frac12\cdot\frac{a\sqrt5}2\cdot a\sqrt2[/math]
[math]h=\frac{\frac{a\sqrt3}2\cdot\frac{a^2}2}{\frac12\cdot\frac{a\sqrt5}2\cdot a\sqrt2}=a\frac{\sqrt3}{\sqrt{10}}=\frac{3\sqrt{30}}5[/math]
Ответ: [math]\frac{3\sqrt{30}}5[/math]
Решите неравенство [math]\frac{\sqrt{\log_2\left(x^2-3\right)}-\sqrt{\log_2\left(x+9\right)}}{\log_2\left(x^2-6x+9\right)}\geq0[/math].
ОДЗ:
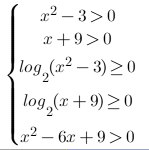
Решение системы: [math]x\in\left[-8;-2\right]\cup\lbrack2;3)\cup(3;+\infty)[/math]
Найдем нули числителя:
[math]\sqrt{log_2(x^2-3)}-\sqrt{log_2(x+9)}=0[/math]
[math]log_2(x^2-3)=log_2(x+9)[/math]
[math]x^2-3=x+9[/math]
[math]x^2-x-12=0[/math]
[math]x_1=-3[/math], [math]x_2=4[/math]
Нули знаменателя: [math]log_2(x^2-6x+9)=0[/math]
[math]x^2-6x+9-1=0[/math]
[math](x-4)(x-2)=0[/math]
[math]x_1=4[/math] – корень кратности 2
[math]x_2=2[/math]
Нанесем нули на числовую прямую и расставим знаки:
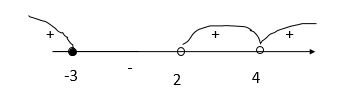
Учитывая ОДЗ, получим: [math]x\in[/math] [-8; -3]⋃(2; 3)⋃(3; 4)⋃(4; +∞)
Ответ: [-8; -3]⋃(2; 3)⋃(3; 4)⋃(4; +∞)
В магазин поступил товар I и II сортов на общую сумму 4,5 млн. руб. Если весь товар продать по цене II сорта, то убытки составят 0,5 млн. руб., а если весь товар реализовать по цене I сорта, то будет полечена прибыль 0,3 млн. руб. На какую сумму был приобретен товар I и II сортов в отдельности?
Пусть x– цена первого сорта, y – цена второго сорта, a – количество первого сорта, b – количество второго сорта. Получим, что в магазин поступило xa+yb=4,5. В первом случае получим следующее уравнение: y(a+b)=4,5-0,5 , во втором случае: x(a+b)=4,5+0,3
В итоге получим систему из трех уравнений:
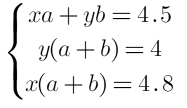
1) Из первого отнимем второе, и из первого отнимем третье.Получится система из двух новых уравнений

Разделим первое на второе: [math]b=\frac35a[/math]
2) Разделим в исхдной системе второе уравнение на первое:[math]y=\frac4{4.8}x[/math]
3) Подставим найденные соотношения в первое уравнение:
[math]xa+\frac4{4.8}x\cdot\frac35a=4.5[/math]
[math]\frac32xa=4.5[/math]
[math]xa=\frac{45\cdot2}{10\cdot3}=3[/math]
4) [math]xa+xb=4.5\Rightarrow xb=4.5-xa=4.5-3=1.5[/math]
Ответ: 3 млн. руб. и 1,5 млн. руб.
К окружности, вписанной в квадрат ABCD, проведена касательная, пересекающая стороны АВ и AD в точках М и Р соответственно.
А) Докажите, что периметр треугольника АМР равен стороне квадрата.
Б) Прямая МР пересекает прямую CD в точке К. Прямая, проходящая через точку К и центр окружности, пресекает прямую АВ в точке Е. Найдите отношение ВЕ:ВМ, если АМ:МВ=1:3.
Решение:
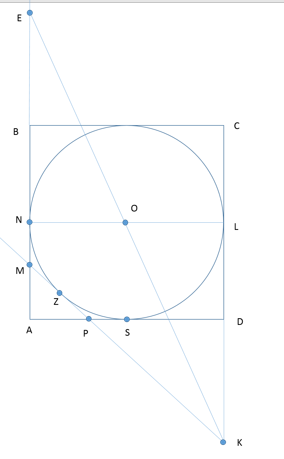
A) [math]P_{\bigtriangleup AMP}=AM+MP+AP[/math]
PS=PZ, NM=MZ. Следовательно по свойств касательных к окружности из одной точки MP=MZ+PZ=MN+PS
AM=AN-MN, AP=AS-PS
[math]P_{\bigtriangleup AMP}=MN+S+AN-MN+AS-PS=AN+AS=2AN=AB[/math] (т.к. NB=AN)
Б) [math]\bigtriangleup ONE=\bigtriangleup OLK[/math] ( по катету и острому углу): ON=OL как радиус окружности, [math]\angle LOK=\angle NOE[/math]
Следовательно, KP=BE (т.к. KP=LK-LD и BE=NE-NB, LK=NE, NB=LD
[math]\bigtriangleup PAM\sim\bigtriangleup PDK[/math] (по двум углам) [math]\angle DPK=\angle APM[/math] как вертикальные , [math]\angle A=\angle D=90^\circ\Rightarrow\frac{DK}{AM}=\frac{DP}{AP}=\frac{BE}{AM}[/math]
AM+MB=AB? MB=3AM. Следовательно 4AM=AB. Значит AM=1/4*AB
[math]P_{\bigtriangleup AMP}=AP+\frac14AB+\sqrt{AP^2+\frac{AB^2}{16}}=AB[/math]
[math]\frac34AB-AP=\sqrt{AP^2+\frac{AB^2}{16}}[/math], [math]\frac9{16}AB^2-\frac32AB\cdot AP+AP^2=AP^2+\frac{AB^2}{16}\Rightarrow\frac32AP=\frac12AB[/math], [math]AP=\frac13AB[/math], [math]PD=\frac23AB[/math]
[math]AM=\frac13BM\Rightarrow\frac{BE}{\frac13BM}=\frac{\frac23AB}{\frac13AB}[/math], [math]\frac{BE}{BM}=\frac23[/math]
Ответ: 2:3
Найдите все а, при каждом из которых система уравнений
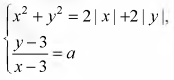
имеет ровно три различных решения.
Решение: преобразуем первое уравнение: [math](\left|x\right|-1)^2+(\left|y\right|-1)^2=2[/math]
Имеем окружность с радиусом [math]R=\sqrt2[/math] и центром О(1,1). Пример применим свойства модулей на графике и получим следующее:

Точка (0;0) тоже входит в график окружности. Чтобы получить гарантированно три решения, должна быть одна точка-фиксированная,т. е получим следующие варианты :

Уравнение прямой: [math]y=ax+(3-3a)[/math]
1 сл: y=0, x=2. Тогда а=3
2 сл: x=0, y=2. Тогда а= 1/3
3 сл: y=0, x=0. тогда а=1
4 и 5 сл: прямая касается одного сектора и пересекает второй в двух точках. Найдем уравнение касательной: [math]x^2-2x+y^2-2y=0[/math]
[math]a_4=-2;a_5=-2;a_6=0[/math]
Получаем уравнение касательной: [math](x_0+\frac{-2}2)x+(\frac{-2}2+y_0)y+(\frac{-2x_0-2y_0}2+0)=0[/math]
[math](x_0+-1)x+(-1+y_0)y+(-x_0-y_0)=0[/math]
Все прямые проходят через точку (3;3), то есть имеем уравнение [math]3(x_0+-1)+3(-1+y_0)+(-x_0-y_0)=0[/math] и исходное уравнение [math]-y_0+ax_0+(-3a+3)[/math]
Решим систему из этих двух уравнение и получим следующие значения:[math]x_0=\frac{3a}{1+a}[/math] [math]y_0=3-\frac{3a}{1+a}[/math]
Подставим в уравнение окружности первого сектора и получим квадратное уравнение: [math]3a^2-12a+3=0[/math]
Решение уравнения: [math]a_{1,2}=2\pm\sqrt3[/math]
Ответ: [math]2-\sqrt3;\;\frac13;\;1;\;3;\;2+\sqrt3[/math]
| № | Ваш ответ | Ответ и решение | Первичный балл |
|---|---|---|---|
|
Здесь появится результат первой части. Нажмите на кнопку «Завершить работу», чтобы увидеть правильные ответы и посмотреть решения. |
|||