Вариант 4
Часть 1.
Ответами к заданиям 1–20 являются число или последовательность цифр, которые следует записать в поле соответствующего задания. Если ответом является последовательность цифр, то запишите её без пробелов, запятых и других дополнительных символов.
Прочитайте внимательно текст и выполните задания 1–5
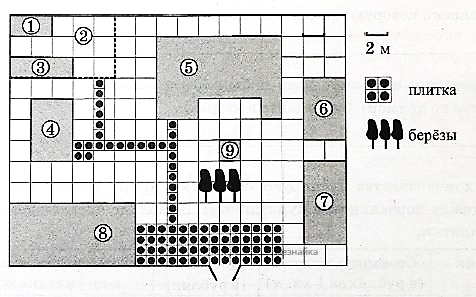
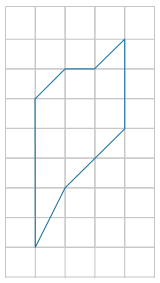
На плане изображено домохозяйство, находящееся по адресу: с. Малые Всегодичи, д. 26. Сторона каждой клетки на плане равна 2 м. Участок имеет форму прямоугольника. Выезд и въезд осуществляются через единственные ворота. При входе на участок справа от ворот находится коровник, а слева — курятник. Площадь, занятая курятником, равна 72 кв. м. Рядом с курятником расположен пруд площадью 24 кв. м. Жилой дом расположен в глубине территории. Перед домом имеется фонтан, а между фонтаном и воротами — небольшая берёзовая рощица. Между жилым домом и коровником построена баня. За домом находится огород (его границы отмечены на плане пунктирной линией), на котором есть теплица, а также (в самом углу и огорода, и всего домохозяйства) — компостная яма.
Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером 1 м х 1 м. Между коровником и курятником имеется площадка площадью 56 кв. м, вымощенная такой же плиткой.
Сопоставьте объекты, указанные в таблице, с цифрами, которыми эти объекты обозначены на плане. Заполните таблицу, а в бланк ответов перенесите последовательность из пяти цифр.
| Объекты | жилой дом | огород | коровник | баня | компостная яма |
| Цифры |
Тротуарная плитка продаётся в упаковках по 3 штуки. Сколько упаковок понадобилось купить владельцам домохозяйства для того, чтобы выложить все дорожки и площадку между коровником и курятником?
Найдите площадь, которую занимает баня. Ответ дайте в квадратных метрах.
Найдите расстояние от жилого дома до пруда (расстояние между двумя ближайшими точками объектов по прямой). Ответ дайте в метрах.
Владельцы домохозяйства планируют обновить всю тротуарную плитку (и дорожки, и площадку между коровником и курятником). В таблице представлены условия трёх поставщиков плитки.
| Поставщик | Стоимость плитки (в руб. за 1 кв.м.) | Доставка (в руб.) | Работы по демонтажу старой плитки и по укладке новой (в руб.) |
| 1 | 440 | 10000 | бесплатно |
| 2 | 430 | 5000 | 3000 |
| 3 | 420 | 2000 | 6000 |
Найдите значение выражения
[math]\frac{8,3-5,7}{1,3}[/math]
Какое из следующих чисел заключено между числами [math]\sqrt{0,23}[/math] и [math]\frac9{17}[/math] ?
1) 0,3
2) 0,4
3) 0,5
4) 0,6
Найдите значение выражения [math](7\cdot10^{-4})(1,3\cdot10^3)[/math]
Решите уравнение [math]49=(2x-7)^2[/math]. Если корней несколько, в ответе укажите наименьший.
В группе 25 человек, из них 10 мальчиков. Среди девочек шесть человек занимаются спортом. Найдите вероятность того, что участник, выбранный на соревнование случайным образом, окажется девочкой, которая не занимается спортом.
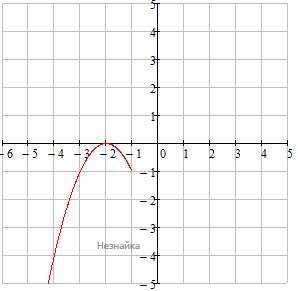
Какой график из приведённых ниже функций изображён на рисунке?
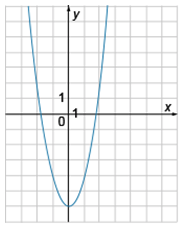
1) [math]2x^2+6[/math]
2) [math]2x^2-6[/math]
3) [math]-2x^2+6[/math]
4) [math]-2x^2-6[/math]
Дана арифметическая прогрессия [math]a_n[/math], разность которой равна 3,2, [math]a_1=-6[/math]. Найдите [math]a_{13}[/math]
Упростите выражение [math]\frac{6x-14}{49-42x+9x^2}[/math] и найдите его значение при х = 2. В ответ запишите полученное число.
Для прямоугольного треугольника справедлива формула [math]c^2=a^2+b^2[/math], где с — гипотенуза, a и b — катеты. Найдите катет b (в см.), если a = 7 см, с = 25 см.
При каких значениях x выражение 6x−2 принимает положительные значения?
1) [math]x>\frac13[/math]
2) [math]x<\frac13[/math]
3) [math]x>3[/math]
4) [math]x<3[/math]
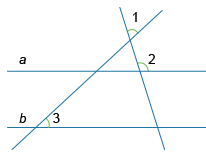
Известно, что прямые a и b параллельны. Найдите угол 1 (в градусах), если известно, что угол 2 равен [math]118^\circ[/math], а угол 3 равен [math]52^\circ[/math].
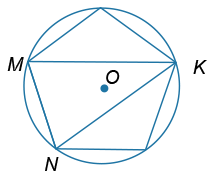
В окружность с центром в точке O вписан правильный пятиугольник. Найдите угол ∠MKN (в градусах).
В равнобедренном треугольнике боковая сторона равна 26 см, а основание — 20 см. Найдите площадь (в см2) этого треугольника.
На клетчатой бумаге с размером клетки 1 см × 1 см изображена фигура. Найдите её площадь (в см2).
Укажите номера неверных утверждений. Выберите 2 варианта из списка.
1) В равнобедренном треугольнике все углы равны.
2) Во всякий четырёхугольник можно вписать окружность.
3) Диагональ параллелограмма делит его на два равных треугольника.
4) Все точки каждой из двух параллельных прямых равноудалены от другой прямой.
Часть 2.
При выполнении заданий 21–26 используйте тетрадь. Сначала укажите номер задания, а затем запишите его решение и ответ. Пишите чётко и разборчиво.
Решите уравнение [math](x^2-25)^2+\left(x^2+3x-10\right)^2=0[/math]
Первый велосипедист выехал из посёлка по шоссе со скоростью 21 км/ч. Через час после него со скоростью 15 км/ч из того же посёлка в том же направлении выехал второй велосипедист, а ещё через час — третий. Найдите скорость третьего велосипедиста, если сначала он догнал второго, а через 9 часов после этого догнал первого.
Постройте график функции
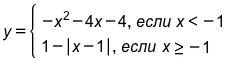
и определите, при каких значениях m прямая y = m имеет с графиком ровно две общие точки.
При х≥-1 Раскроем знак модуля: х-1=0 → х0=1 При -1≤х≤1: у=1-(1-х) → у=х - прямая, биссектриса 1 и 3 четверти, выходит из начала координат. При х>1: у=1-(х-1) → у=2-х - прямая (у=-х), сдвинутая на 2 ед вправо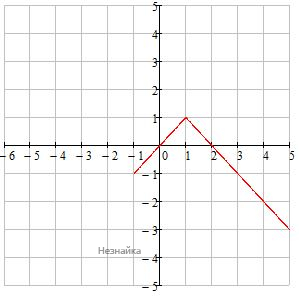 
Совмещаем 
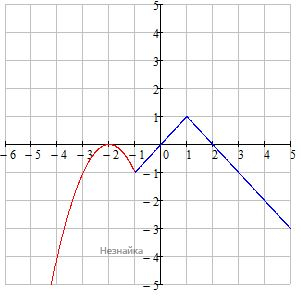Прямая y=m параллельна оси ОХ и пересекает график в двух точках только при у<-1 и 0<у<1 Ответ: ує(-∞;-1), (0;1)Меньшее основание прямоугольной трапеции равно 12,5 см, а большая диагональ является биссектрисой угла при большем основании и равна 20 см. Найдите площадь трапеции.
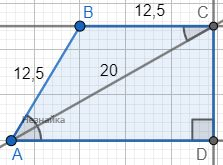AD и BC - параллельны, так что ∠CAD=∠ACB как накрест лежащие. Тогда △ABC равнобедренный и AB=BC. По теореме косинуса найдем косинус угла ∠BAC: [math]cos\angle BAC=\frac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}=\frac{12,5^2+20^2-12,5^2}{2\cdot12,5\cdot20}=0,8[/math] [math]cos\angle BAC=cos\angle CAD=\frac{AD}{AC}=0,8[/math] → [math]AD=AC\cdot cos\angle CAD=20\cdot0,8=16[/math] По теореме Пифагора найдем высоту трапеции CD: CD=√(AC2-AD2)=√(202-162)=12 [math]S=\frac{BC+AD}2\cdot CD=\frac{12,5+16}2\cdot12=171[/math] Ответ: 171В треугольнике АВС угол АСВ тупой, ВО[math]\perp[/math]АС, OF[math]\perp[/math]AB, OD[math]\perp[/math]BC. Докажите, что [math]\angle[/math]ACB = [math]\angle[/math]DFB.
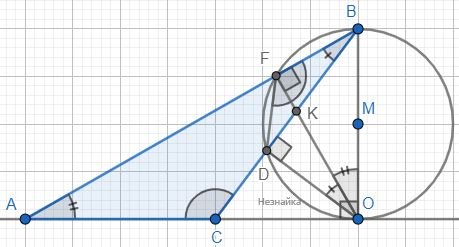Треугольники △OFB и △AOB подобны, так как они прямоугольные и ∠OBF общий. Значит углы ∠BOF=∠BAO равны между собой. Треугольники △ODK и △BFK так же подобны - они прямоугольные и ∠FKB=∠DKO. Тогда равны углы ∠DOK=∠FBK. Углы ∠ODB и ∠OFB прямые, поэтому можно построить окружность на OB, как на диаметре, и при этом точки D и F лежат на этой окружности. То есть четырехугольник ODFB - вписанный в окружность, и значит сумма противоположных углов равна 180°. ∠DFB+∠DOB=180° ∠DFB=180°-∠DOB=180°-(∠DOK+∠BOF)=180°-(∠FBK+∠BAO)=∠ACB ∠ACB=180°-(∠FBK+∠BAO) → ∠DFB=∠ACBВ выпуклом четырёхугольнике ABCD точка Е – точка пересечения диагоналей. Известно, что площадь каждого из треугольников АВЕ и DСЕ равна 1, площадь четырёхугольника АВСD не превосходит 4, АD = 3. Найдите длину стороны ВС.
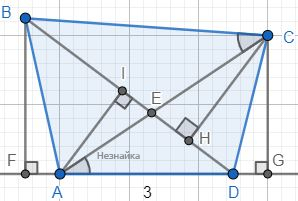Площади треугольников △ABD и △ACD равны между собой, так как : S△ABD=S△ABE+S△AED S△ACD=S△DEC+S△AED S△ABE=S△DEC=1 Тогда S△ABD=S△ACD , т.е. 1/2⋅BF⋅AD=1/2⋅CG⋅AD → BF=CG → BF и CG перпендикулярны AD → AD параллельно BC → ABCD - трапеция ∠DAC=∠ACB - как накрестлежащие → △AED подобен △CEB [math]\frac{AD}{BC}=\frac{DE}{BE}=\frac{CE}{AE}[/math] Рассмотрим треугольники △BCE и △DCE : S△BCE=1/2⋅CH⋅BE S△DCE=1/2⋅CH⋅DE [math]\frac{S_{\bigtriangleup BCE}}{S_{\bigtriangleup DCE}}=\frac{BE}{DE}=\frac{BC}{AD}[/math] → S△BCE=BC/3 Рассмотрим треугольники △BAE и △AED : S△ABE=1/2⋅AI⋅BE S△AED=1/2⋅AI⋅DE [math]\frac{S_{\bigtriangleup ABE}}{S_{\bigtriangleup AED}}=\frac{BE}{DE}=\frac{BC}{AD}[/math] → S△AED=3/BC Так как SABCD≤4 , то S△AED+S△BCE+S△ABE+S△BCE≤4 3/BC+BC/3+1+1≤4 BC/3-2+3/BC≤0 BC2-6⋅BC+9≤0 (BC-3)2≤0 → BC=3 так как квадрат числа не может быть отрицательным, но может быть равен 0. Ответ: 3| № | Ваш ответ | Ответ и решение | Первичный балл |
|---|---|---|---|
|
Здесь появится результат первой части. Нажмите на кнопку «Завершить работу», чтобы увидеть правильные ответы и посмотреть решения. |
|||