Вариант 7
Математика Профильный уровень
Часть 1
Ответом на задания 1—12 должно быть целое число или десятичная дробь.
Компания для украшения помещения к новому году закупила 7 искусственных ёлок. Для украшения одной ёлки требуется не менее 13 игрушек. Игрушки продаются комплектами по 10 штук. Сколько нужно закупить комплектов, чтобы украсить все ёлки?
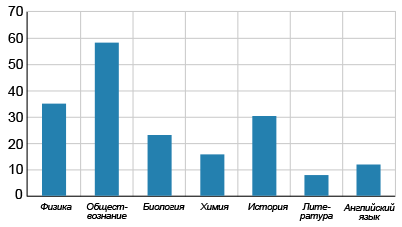
На диаграмме изображено количество учеников 11 класса, выбравших для сдачи ЕГЭ различные дополнительные экзамены. По горизонтали указаны экзамены, по вертикали — количество учеников, выбравших тот или иной экзамен. По диаграмме определите, сколько экзаменов были более востребованы, чем химия.
Найдите площадь равнобедренной трапеции (в см2), высота которой равна 7 см и делит основание на отрезки длиной 17 см и 6 см.
На производстве при упаковке чая вероятность того, что упаковка окажется не герметичной, равна 0,09. Найдите вероятность того, что две произвольно выбранные упаковки чая окажутся герметичными.
Решите уравнение [math]\sqrt{\frac{3x-5}{2x}}=\frac13[/math]
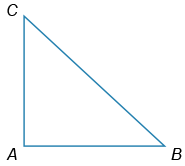
В прямоугольном треугольнике ABC угол A равен 90°. Найдите сторону AC (в см), если tg∠C=[math]\frac74[/math], CB=[math]2\sqrt{65}[/math] см.
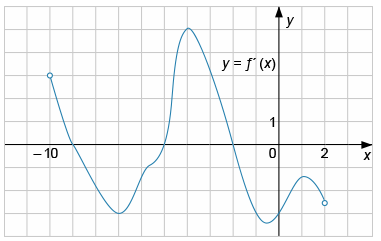
На рисунке представлен график производной функции y=f '(x) на интервале (−10; 2). Найдите точку минимума функции y=f(x) на данном промежутке.
Объём прямоугольного параллелепипеда, в основании которого лежит квадрат, равен 200 см3. Найдите площадь его боковой поверхности (в см2), если высота параллелепипеда равна 8 см.
Найдите значение выражения [math]\frac{log_5125}{log_\frac139}[/math]
Координата тела при равноускоренном движении изменяется по закону [math]x=x_0+v_0t+\frac{at^2}2[/math], где [math]x_0[/math] — начальная координата тела, a — ускорение тела, t — время движения тела. Найдите время движения тела, если его ускорение равно 2 м/c2, начальная координата равна 7 м, а координата в конце движения равна 67 м при начальной скорости 11 м/с.
Из одного порта в другой по течению выплыл плот, через два часа ему навстречу выплыла моторная лодка, они встретились через 4 часа после отправления лодки. Найдите скорость лодки (в км/ч), если скорость течения равна 3 км/ч, а расстояние между портами равно 146 км.
Найдите наименьшее значение функции [math]y=4x+\frac1x+7[/math] на промежутке (0;2)
Часть 2.
При выполнении заданий 13—19 требуется записать полное решение и ответ.
Дано уравнение 4cos4x - 5cos2x - 1 = 0.
А) Решите уравнение.
Б) Укажите корни этого уравнения, принадлежащие отрезку [arccos0; arccos(-1)].
А) Преобразуем уравнение:
[math]4(\frac{1+cos2x}2)^2-5cos2x-1=0[/math]
[math]1+2cos2x+cos^22x-5cos2x-1=0[/math]
[math]cos^22x-3cos2x=0[/math]
[math]cos2x(cos2x-3)=0[/math]
т.е. имеем, что [math]cos2x=0[/math] или [math]cos2x-3=0[/math]
В первом случае [math]2x=\frac\pi2+\pi n[/math]; [math]x=\frac\pi4+\frac{\pi n}2[/math], [math]n\in Z[/math]
Во втором случае [math]\varnothing[/math], так как не соответствует области значений косинуса
Б) Нанесем корни на числовую прямую и определим, какие корни входят в отрезок:
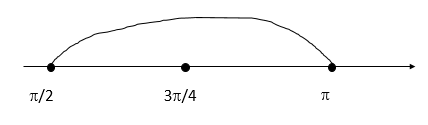
Ответ:
А) [math]\frac\pi4+\frac{\pi k}2;\;k\in Z;[/math]
Б) [math]\frac{3\pi}4[/math]
Цилиндр и конус имеют общее основание, вершина конуса является центром другого основания цилиндра. Каждая образующая конуса наклонена к плоскости основания под углом 30°.
А) Докажите, что площади боковых поверхностей цилиндра и конуса равны.
Б) Найдите радиус сферы, касающейся боковых поверхностей цилиндра и конуса, а также одного из оснований цилиндра, если известно, что объем конуса равен [math]\left(6\sqrt3+10\right)\cdot\pi[/math].
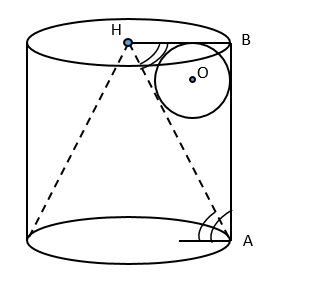
А) [math]S_{б.к.}=S_{б.ц.}[/math] - доказать
[math]S_{б.к.}=\pi r\cdot AH[/math] ; [math]S_{б.ц.}=2\pi r\cdot AB[/math]
Рассмотрим [math]\bigtriangleup ABH[/math], [math]H[/math] - центр основания цилиндра, [math]BA\perp[/math] нижнему основанию цилиндра, [math]\angle B=90^\circ[/math]
[math]sin(\angle H)=\frac{AB}{AH}=sin(30^\circ)=\frac12\Rightarrow AB=\frac12AH[/math]
[math]\Rightarrow S_{б.ц.}=2\pi r\cdot\frac12AH=\pi r\cdot AH=S_{б.к.}[/math], что и требовалось доказать
Б) [math]V_к=(6\sqrt3+10)\pi[/math], [math]r_0[/math] - ?
т. [math]О[/math] - центр сферы, пусть т. [math]O\in(ABH)[/math]
[math]\Rightarrow r_0=[/math] радиусу вписанное в [math]\bigtriangleup ABH[/math] окружности
[math]\Rightarrow r_0=\frac{HB+AB-AH}2=\frac{R+h-\frac h{sin(\angle H)}}2=\frac{R-h}2[/math]
[math]\frac hR=tg(\angle H)\Rightarrow h=R\cdot tg(30^\circ)=\frac{R\sqrt3}3[/math]
[math]V_к=\frac13\pi R^2h=\frac13\pi R^2\cdot\frac{R\sqrt3}3=\frac{\pi R^3\sqrt3}9[/math], [math]r_0=\frac{R(1-\frac{\sqrt3}3)}2\Rightarrow R=\frac{2r_0}{1-\frac{\sqrt3}3}[/math]
[math]\Rightarrow\frac{\pi\sqrt3}9\cdot(\frac{2r_0}{1-\frac{\sqrt3}3})^3=(6\sqrt3+10)\pi[/math]
[math]\frac{8\sqrt3}9r_0^3=12\sqrt3-20+20-\frac{100\sqrt3}9[/math]
[math]r_0^3=1[/math]
[math]r_0=1[/math]
Ответ: 1
Решите неравенство [math]\frac{\log_3\sqrt{28\cdot3^x-3}}{x+1}\geq1[/math].
Перенесем единицу в левую часть и приведем к общему знаменателю:
[math]\frac{log_3\sqrt{28\cdot3^x-3}-(x+1)}{x+1}\geq0[/math]
ОДЗ: [math]28\cdot3^x-3>0[/math]
[math]x>log_3\frac3{28}[/math]
[math]x>1-log_328[/math]
Нули числителя: [math]\frac12log_3(28\cdot3^x-3)-(x+1)=0[/math]
[math]log_3(28\cdot3^x-3)=2(x+1)[/math]
[math]28\cdot3^x-3=3^{2(x+1)}[/math]
[math]9\cdot3^{2x}-28\cdot3^x+3=0[/math]
D=646
[math]3^x=\frac{28+26}{18}=3\Rightarrow x=1[/math]
[math]3^x=\frac{28-26}{18}=\frac19\Rightarrow x=-2[/math]
Нули знаменателя:[math]x+1=0\Rightarrow x=-1[/math]
Нанесем нули на числовую прямую, расставим знаки, при этом учитываем ОДЗ:
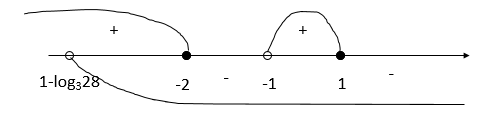
Ответ: (1-log328; -2]⋃(-1; 1]
В прямоугольном треугольнике АВС известно, что ВС=2⋅АС. На гипотенузе АВ вне треугольника построен квадрат ABEF. Прямая СЕ пересекает АВ в точке О.
А) Докажите, что ОА:ОВ=3:4.
Б) Найдите отношение площадей треугольников АОС и ВОЕ.
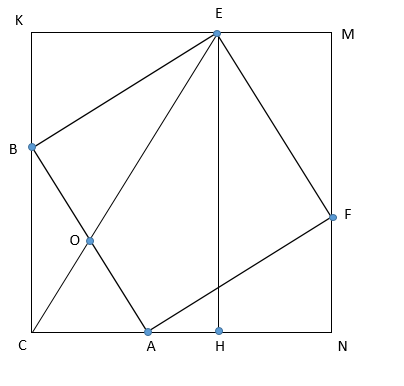
А) Достроим до квадрата [math]CKMN[/math] так, чтобы [math]\bigtriangleup ABC=\bigtriangleup FAN=\bigtriangleup EFM=\bigtriangleup BEK[/math]
Обозначим [math]\angle OCA=\alpha[/math] и запишем теорему синусов для [math]\bigtriangleup OCA[/math] и [math]\bigtriangleup OCB[/math]:
[math]\frac{OC}{sin(\angle OBC)}=\frac{OB}{sinn(90^\circ-\alpha)}[/math]
[math]\Rightarrow\frac{OA}{OB}\cdot\frac{cos\alpha}{sin\alpha}=\frac{sin(\angle OBC)}{sin(\angle OAC)}[/math]
[math]\Rightarrow\frac{OA}{OB}=\frac{sin(\angle OBC)}{sin(\angle OAC)}\cdot tg\alpha[/math]
Опустим из Е перпендикуляр на CN. [math]EH\perp CN;EH=MN=CA+BC=3AC[/math]
[math]HN=EM[/math] (по свойству прямоугольника [math]EMNH[/math])
[math]\Rightarrow CH=CN-HN=3AC-AC=2AC[/math]
[math]\Rightarrow tg(\angle ECH)=tg\alpha=\frac32[/math]
Рассмотрим [math]\bigtriangleup ABC[/math]: по теореме Пифагора [math]AB=\sqrt{AC^2+BC^2}=\sqrt{AC^2+4AC^2}=\sqrt5AC[/math]
[math]sin(\angle ABC)=sin(\angle OBC)=\frac{AC}{\sqrt5AC}=\frac1{\sqrt5}[/math]
[math]sin(\angle BAC)=sin(\angle OAC)=\frac{2AC}{\sqrt5AC}=\frac2{\sqrt5}[/math]
[math]\Rightarrow\frac{OA}{OB}=\frac1{\sqrt5}\cdot\frac{\sqrt5}2\cdot\frac32=\frac34[/math], ч.т.д.
Б) [math]\frac{S_{\bigtriangleup AOC}}{S_{\bigtriangleup BOE}}-?[/math]
[math]S_{\bigtriangleup AOC}=\frac12AO\cdot AC\cdot sin(\angle AOC)=\frac12\cdot\frac37AB\cdot AC\cdot\frac2{\sqrt5}=\frac3{7\sqrt5}AC\cdot\sqrt5\cdot AC=\frac37AC^2[/math]
[math]S_{\bigtriangleup BOE}=\frac12BO\cdot BE=\frac12\cdot\frac47\cdot AB\cdot AB=\frac27\cdot\left(AC\sqrt5\right)^2=\frac{10}7AC^2[/math]
[math]\Rightarrow\frac{S_{\bigtriangleup AOC}}{S_{\bigtriangleup BOE}}=\frac{\frac37AC^2}{\frac{10}7AC^2}=\frac3{10}[/math]
Ответ: 0,3
16 ноября близнецы Саша и Паша взяли в банке кредит по 500 тысяч руб. каждый сроком на четыре месяца. Условия возврата кредита таковы:
• 28-го числа каждого месяца долг увеличивается на 10 % по сравнению с 16-м числом текущего месяца;
• с 1-го по 15-е число каждого месяца необходимо выплатить часть долга; 16-го числа каждого месяца долг должен составлять некоторую сумму в соответствии с предложенной для каждого из них таблицей:
Саша
| Дата | 16.11 | 16.12 | 16.01 | 16.02 | 16.03 |
| Долг, тыс. руб. | 500 | 300 | 200 | 100 | 0 |
Паша
| Дата | 16.11 | 16.12 | 16.01 | 16.02 | 16.03 |
| Долг, тыс. руб. | 500 | 400 | 300 | 200 | 0 |
Kто из братьев за четыре месяца выплатит банку меньшую сумму? На сколько рублей?
Решение:
Составим таблицу выплат каждого из близнецов и посчитаем итоговую сумму выплаты по каждому:
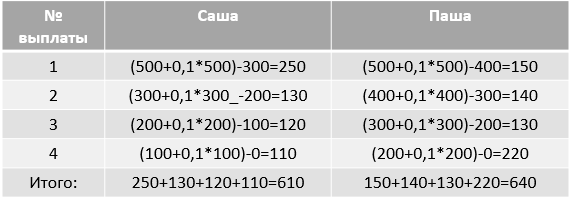
Получим, что Саша выплатит меньше на 30 тыс. ( 640-610=30)
Ответ: Саша выплатит меньше на 30 тыс.
Найдите все а, при каждом из которых в область значений функции [math]y=\frac{8x-a-6}{8x^2+8}[/math] входит ровно два целых числа. Для каждого такого а укажите эти целые числа.
Решение: так как нам дана дробь, и числитель является линейной функцией , то какое бы a мы не взяла всегда найдется значение х, в котором числитель равен 0, соответственно и исходная функция. ( такой же вывод можно сделать из предела функции)
Исходная функция непрерывна на [math]x\in R[/math]. Требуется по условию, что в область значений входит только два целых числа, значит имеем два варианта: 0 и 1, 0 и -1. Рассмотрим два случая.
1 сл: 0 и 1
Решим уравнение:
[math]\frac{8x-a-6}{8x^2+8}=1[/math]
[math]8x^2-8x+a+14=0[/math]
[math]D=64-32(a+14)\geq0[/math]
[math]a\leq-12[/math]
Учтем, что значения функции в данном случае лежит в пределах [math](-1;2)[/math] при [math]x\in R[/math]
Решим неравенство [math]-1<\frac{8x-a-6}{8x^2+8}<2[/math].
Решение: [math]a>-21;a<0[/math]. Получим, учитывая область значений функции, что [math]a\in(-21;-12\rbrack[/math]
2 сл: 0 и -1
Решим уравнение:
[math]\frac{8x-a-6}{8x^2+8}=-1[/math]
[math]8x^2+8x-a+2=0[/math]
[math]D=64-32(-a+2)\geq0[/math]
[math]a\geq0[/math]
Учтем, что значения функции в данном случае лежит в пределах [math](-2;1)[/math] при [math]x\in R[/math]
Решим неравенство [math]-2<\frac{8x-a-6}{8x^2+8}<1[/math].
Решение: [math]a>-12;a<9[/math]. Получим, учитывая область значений функции, что [math]a\in\lbrack0;9)[/math]
Ответ: a∈(-21; -12]⋃[0; 9);
при а∈(-21; -12] y=0 и y=1;
при а∈[0; 9) y=0 и y=-1
А) Каждая точка плоскости окрашена в один из двух цветов. Обязательно ли на плоскости найдутся две точки одного цвета, удаленные друг от друга ровно на 1 м?
Б) Каждая точка прямой окрашена в один из 10 цветов. Обязательно ли на прямой найдутся две точки одного цвета, удаленные друг от друга на целое число метров?
В) Какое наибольшее количество вершин куба можно покрасить в синий цвет так, чтобы среди синих вершин нельзя было выбрать три, образующие равносторонний треугольник?
А) Предположим, что для произвольной точки плоскости все точки, удаленные от нее ровно на 1 м, другого цвета (если среди них были бы точки того же цвета, то это бы означало, что для этой произвольной точки нашлась точки того же цвета и задача была решена изначально). Следовательно, мы получим окружность радиуса 1 м, центр которой - точка одного цвета, а все точки окружности - точки другого цвета. На окружности всегда найдется хорда, равная радиусу окружности, следовательно мы найдем две точки одного цвета ( на концах хорды), отстоящих друг от друга на длину хорды, т.е. 1м. Ответ : да, можно
Б) Вероятность точки прямой определенного цвета 1/10. Следовательно из 20 точек прямой точки одного цвета попадут минимум 2 раза. Разместим точки разных десяти цветов на одинаковом целочисленном расстоянии друг от друга, тогда 11 точка будет совпадать с цветом любой из предыдущих, так как точки размещены всех 10ти цветов. Значит ответ:да, можно
В) Можно выбрать 4 вершины (вершины одной грани, они не образуют равносторонний треугольник). Если берем пять вершин, то можно составить равносторонний треугольник. На рисунке приведено решение:
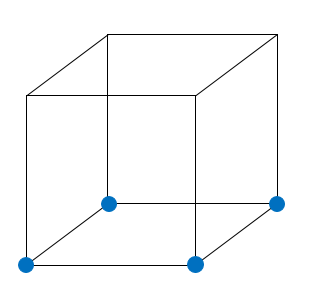
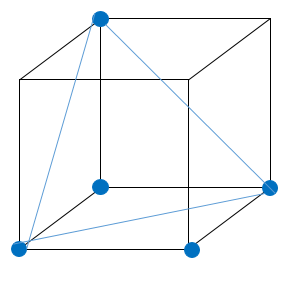
Ответ: А) да; Б) да; В) 4.
| № | Ваш ответ | Ответ и решение | Первичный балл |
|---|---|---|---|
|
Здесь появится результат первой части. Нажмите на кнопку «Завершить работу», чтобы увидеть правильные ответы и посмотреть решения. |
|||