Вариант 19
Математика Профильный уровень
Часть 1
Ответом на задания 1—11 должно быть целое число или десятичная дробь.
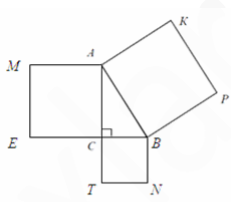
В треугольнике АВС угол С равен 90º. Площади квадратов АВРК и АСЕМ равны 16 и 12 соответственно. Найдите площадь квадрата СВNT.
Найдите длину веĸтора [math]\vec c\left\{6\;;\;8\right\}[/math].
Три ребра прямоугольного параллелепипеда, выходящие из одной вершины раннь 5, 7, 10. Найдите диагональ параллелепипеда.
В турнире по шахматам приняли участие 20 мальчиков. Известно, что троих из них зовут Пётр, двоих — Иван, а остальные участники турнира носят другие имена. Какова вероятность того, что победителя турнира зовут Иван или Пётр?
Вероятность попасть в мишень равна 0,7. Произведено три выстрела. Какова вероятность, что мишень была поражена ровно два раза?
Найдите корень уравнения
[math]\frac{3^x}{\sqrt3}=\frac19[/math]
Найдите значение выражения
[math]\frac{log_{25}2}{log_{125}2}[/math]
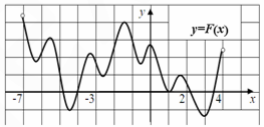
На рисунке изображён график функции y = F(x) − одной из первообразных некоторой функции f(x), определённой на интервале (‐7;4). Пользуясь рисунком, определите значение функции f(x) в точке х=1.
Максимальная высота подъёма тела, брошенного под углом к горизонту, вычисляется по формуле [math]h=\frac{(v\cdot sin\alpha)^2}{2g}[/math] где v (м/c) – начальная скорость тела, α – угол, под которым тело брошено к горизонту, g – ускорение свободного падения (считать, что g=10 м/ 2). С какой скоростью необходимо бросить мяч под углом 30º к горизонту, чтобы он поднялся на высоту 4 м 5 см?
Одна бригада может убрать поле за 12 дней, а другая выполняет ту же работу за 75% времени, необходимого первой бригаде. После того как в течение 5 дней работала первая бригада, к ней присоединилась вторая и они вместе закончили работу. Сколько дней бригады работали вместе?
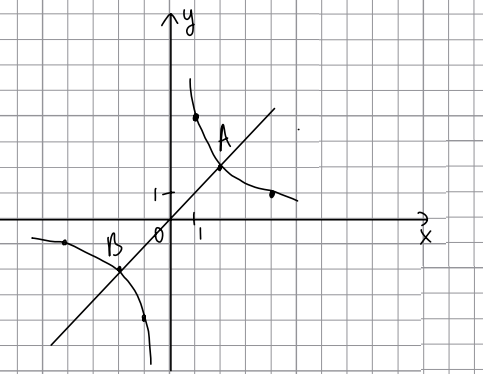
На рисунĸе изображены графики функций [math]f\left(x\right)=\frac ax\;\;и\;\;g(x)=kx+b[/math], которые пересекаются в точках A и B. Найдите сумму абсциссы и ординаты точки B.
Часть 2.
При выполнении заданий 12—18 требуется записать полное решение и ответ.
Найдите точку минимума функции [math]f(x)=x^2-3,75x-ln(x+2)[/math]
Область определения данной функции: х+2>0 —-> x>-2
Найдем производную:
(x2-3,75x-ln(x+2))'=2x-3,75-1/(x+2)
Находим экстремумы:
2x-3,75-1/(x+2)=0
(2x2+0,25x-8,5)/(x+2)=0
8x2+x-34=0
D=12-4∙8∙(-34)=1089
x1=(-1-√1089)/(2∙8)=-2,125 — не входит в область определения функции
x2=(-1+√1089)/(2∙8)=2 — ясно/понятно, что это точка минимума
Дано уравнение [math]\sqrt{0,5+sin^2x}+cos2x=1[/math]
а) решите уравнение
б) Найдите его корни, принадлежащие отрезку 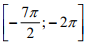

В основании прямой призмы ABCA1B1C1 лежит прямоугольный треугольник АВС гипотенузой АВ, причем АВ=АА1. Через точку В1 перпендикулярно СА1 проведена плоскость α.
а) Докажите, что сечением призмы плоскостью α является прямоугольный треугольник.
б) Найдите объем большей части призмы, на которые ее делит плоскость α, если известно, что АС=8, ВС=6.
Решите неравенство [math]\frac1{log_2(x^4-8x^2+16)-log_2^2(4-x^2)}\leq1[/math]
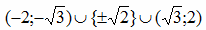
1 июня планируется взять кредит в банке на сумму 6 млн. рублей на срок 12 месяцев. Условия возврата таковы:
— 15 числа каждого месяца долг возрастает на r % (r – целое число) по сравнению с началом текущего месяца;
— с 16 по 28 число необходимо выплатить часть долга так, чтобы на начало каждого следующего месяца долг уменьшался на одну и ту же сумму по сравнению с предыдущим месяцем.
Найдите наименьшую возможную ставку r, если известно, что в декабре банку будет выплачено более, чем на 100 тыс. руб. больше, нежели в марте.
7
На стороне АС треугольника АВС отметили точку D так, что [math]BC=\sqrt{AC\cdot CD}[/math]
а) Докажите, что углы BAD и СВD равны.
б) Найдите отношение отрезков биссектрисы СL треугольника АВС, на которые ее делит прямая ВD, если известно, что ВС=6, АС=9.
2
Найдите все значения параметра а, при каждом из которых уравнение [math]4^{\vert x\vert}+a\cdot2^{\vert x\vert+2}=6a^2-13a+5[/math] имеет ровно два корня.
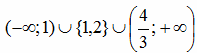
| № | Ваш ответ | Ответ и решение | Первичный балл |
|---|---|---|---|
|
Здесь появится результат первой части. Нажмите на кнопку «Завершить работу», чтобы увидеть правильные ответы и посмотреть решения. |
|||