Вариант 18
Математика Профильный уровень
Часть 1
Ответом на задания 1—11 должно быть целое число или десятичная дробь.
Найдите угол BAC треугольника ABC, если известны координаты его вершин: A(3; 3), B(3; 9), C(6; 6). Ответ запишите в градусах.
Длина веĸтора [math]\vec b[/math] равна 13.
Координаты [math]\vec b\left\{5\;;\;y\right\}[/math]. Найдите [math]y,\;если\;y<{}.[/math]
Три ребра прямоугольного параллелепипеда, выходящие из одной вершины раннь 5, 7, 10. Найдите S поверхности параллелепипеда.
На столе лежат цветные ручки: синяя, красная, чёрная и зелёная. Петя случайно берёт со стола ручку. С какой вероятностью эта ручка окажется чёрной?
Аттестационный экзамен в автошколе состоит из двух этапов: теории и практики. Вероятность сдать теорию равна 0,8, а вероятность сдать практику равна 0,65. Найдите вероятность сдать аттестационный экзамен в автошколе.
Найдите наименьший корень уравнения [math]\sqrt{x^2-4x+4}=2[/math]
Найдите значение выражения [math](log_65)(log_54+log_59)[/math]
Определите количество точек экстремума функции [math]y=3x^4-8x^3[/math]
Радиус окружности, вписанной в прямоугольный треугольник, можно найти по формуле [math]r=\frac{ab}{a+b+\sqrt{a^2+b^2}}[/math], где a и b катеты прямоугольного треугольника. Чему равна длина гипотенузы c (в см), если радиус окружности, вписанной в этот прямоугольный треугольник, равен 1 см, а один из катетов равен 4 см?
Сельский житель Андрей Иванович может убрать свой урожай картофеля за 3 часа, если будет работать один, а если ему будут помогать двое его сыновей, то они вместе смогут убрать этот урожай за 2 часа. За какое время (в часах) уберут весь урожай два сына Андрея Ивановича и соседский мальчишка, если производительность всех трёх ребят одинакова?
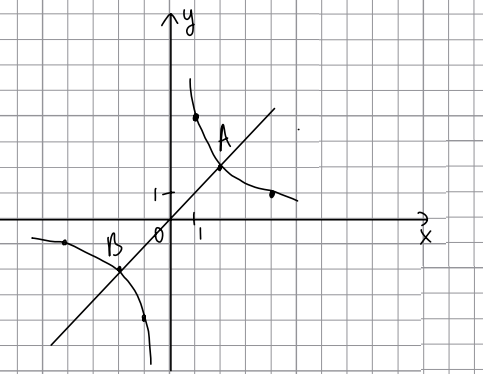
На рисунĸе изображены графики функций [math]f\left(x\right)=\frac ax\;\;и\;\;g(x)=kx+b[/math], которые пересекаются в точках A и B. Найдите ординату B.
Часть 2.
При выполнении заданий 12—18 требуется записать полное решение и ответ.
Найдите минимум функции [math]y=\frac{x^2+3}{\sqrt x}[/math]
Область определения функции: [math]x>0[/math]
Найдем производную функции
[math]y'=\left(\frac{x^2+3}{\sqrt x}\right)^,=\frac{2x\cdot\sqrt x-\frac1{2\sqrt x}\cdot(x^2+3)}x=\frac{3(x^2-1)}{x\sqrt x}[/math]
x=1 - единственный экстремум, удовлетворяющий области определения, при переходе через который производная меняет свой знак с отрицательного на положительный.
Дано уравнение [math]2\cos x-3\sqrt{2\cos x}+2=0[/math].
а) Решите уравнение.
б) Укажите корни этого уравнения, принадлежащие промежутку [math]\left[-\frac{7\pi}2;\;-2\pi\right][/math].
а) [math]\pm\frac\pi3+2\pi k;[/math] б) [math]-\frac{7\pi}3[/math]
В правильной треугольной пирамиде SABC сторона основания равна 6, а боковое ребро равно 5. На ребре SC отмечена точка М так, что SM:MС=7:18.
а) Докажите, что плоскости SBC и АВМ перпендикулярны.
б) Найдите объем меньшей части пирамиды SABC, на которые ее разбивает плоскость АВМ.
[math]\frac{21\sqrt{39}}{25}[/math]
Решите неравенство [math]\frac{x^2-x+1}{x-1}+\frac{x^2-3x-1}{x-3}\leq2x+2[/math].
[math]\left(-\infty;\;1\right)\cup\left\{2\right\}\cup\left(3;\;+\infty\right)[/math]
1 августа 2016 года Валерий открыл в банке счёт «Пополняй» на четыре года под 10% годовых, вложив 100 тыс. рублей.
1 августа 2017 и 1 августа 2019 года он планирует докладывать на счёт по n тыс. рублей. Найдите наименьшее целое n, при котором к 1 августа 2020 года на счету у Валерия окажется не менее 200 тыс. рублей.
23
В остроугольном треугольнике АВС проведены высоты АК и ВР.
а) Докажите, что углы АКР и АВР равны.
б) Найдите длину отрезка РК, если известно, что АВ=5, ВС=6, СА=4.
[math]\frac{45}{16}[/math]
Найдите все а, при каждом из которых уравнение [math]\frac{2a^2-\left(x+3\right)a-x^2+3x}{x^2-9}=0[/math] имеет ровно один корень.
-3; 0; 1
| № | Ваш ответ | Ответ и решение | Первичный балл |
|---|---|---|---|
|
Здесь появится результат первой части. Нажмите на кнопку «Завершить работу», чтобы увидеть правильные ответы и посмотреть решения. |
|||