Вариант 16

Найдите бо́льший угол ромба, если меньшая диагональ равна [math]\sqrt6[/math] см, а большая диагональ равна [math]3\sqrt2[/math] см. Ответ дайте в градусах.

Найдите длину веĸтора [math]\vec b=\left\{5\;;\;12\right\}[/math].

В ĸуб вписан шар. Диаметр шара равен 8. Найдите объем ĸуба

Механические часы с двенадцатичасовым циферблатом в какой-то момент остановились. Найдите вероятность того, что часовая стрелка остановилась, достигнув отметки 2, но не дойдя до отметки 5.

В столовую школы пришла партия из 1200 пачек печенья. Оказалось, что 15 из них имеют дефектную упаковку. Какова вероятность того, что случайно выбранная пачка печенья не будет иметь дефектную упаковку?

Решите уравнение [math]log_3x=log_936[/math].

Найдите значение выражения [math]\sqrt[3]a+1[/math], если [math]\sqrt[6]a=6[/math].

К графику функции [math]y\;=\;x^2-3x[/math] провели касательную в точке [math]x_0=3[/math]. Найдите ординату точки пересечения этой касательной с осью OУ.

Фокусное расстояние F собирающей линзы определяют по формуле Декарта [math]\frac1F=\frac1d+\frac1f[/math], где d — расстояние от линзы до предмета, а f — расстояние от линзы до действительного изображения. Известно, что расстояние от линзы до предмета равно 60 см, а расстояние от линзы до изображения равно 40 см. Чему равно главное фокусное расстояние F? Ответ запишите в сантиметрах.

Имеются два сплава олова. Масса первого сплава меньше массы второго на 2 кг. Из этих двух сплавов получили третий сплав, содержащий 12 % олова. Найдите массу второго сплава (в кг), если первый сплав содержит 15 % олова, а второй — 10 % олова.

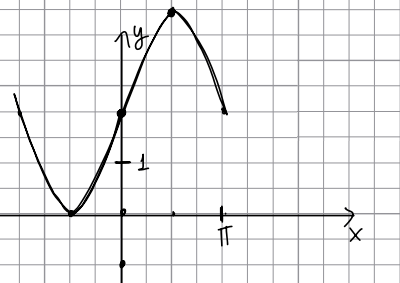
На рисунке изображен график [math]f\left(x\right)=a\sin x+b[/math]. Найдите a.

Найдите точку максимума функции [math]y\;=-x^3+3x^2+24x-18[/math]

Дано уравнение 625^x-6⋅125^x+9⋅25^x=4⋅25^x-24⋅5^x+36.

а) Решите уравнение.

б) Укажите его корни из отрезка [math]\left[\frac13;\;\frac12\right][/math]

Дана правильная шестиугольная призма ABCDEFA₁B₁C₁D₁E₁F₁. Через точки B, D₁, F₁ проведена плоскость α.

а) Докажите, что плоскость α пересекает ребро CC₁в такой точке М, что MC:MC₁=1:2.

б) Найдите отношение объемов многогранников, на которые данную призму делит плоскость α.

Решите неравенство [math]\frac{5\left(x-6\sqrt x+8\right)}{x-16}\leq\sqrt x-2[/math].

В распоряжении прораба Валерия имеется бригада каменщиков в составе 40 человек. Их нужно распределить на неделю на два строящихся объекта.

Если на первом объекте работает t человек, то их недельная зарплата составляет 1,5t² тыс. рублей.

Если на втором объекте работает t человек, то их недельная зарплата составляет 2t² тыс. рублей.

Как Валерию нужно распределить на эти объекты бригаду каменщиков, чтобы выплаты на их недельную зарплату оказались наименьшими? Сколько рублей в этом случае пойдет на зарплату?

Четырехугольник АВСD со взаимно перпендикулярными диагоналями АС и BD вписан в окружность.

А) Докажите, что квадрат диаметра окружности равен сумме квадратов противоположных сторон четырехугольника.

Б) Найдите площадь четырехугольника АВСD, если известно, что АВ = √5, BC = √2, CD = √7.

Найдите все а, при каждом из которых уравнение [math]2\cos2x+2a\sin x+a-1=0[/math] имеет наибольшее количество решений на отрезке [math]\left[-\pi;\;\frac{17\pi}6\right][/math]. Чему равно это количество?