Вариант 15

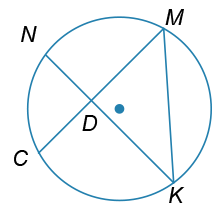
В окружности хорды NK и MC пересекаются под прямым углом в точке D. Найдите угол DKM (в градусах), если дуга KC, содержащая точки N и M, равна 260°.

Координаты веĸтора [math]\vec a\;\left\{7\;;\;10\right\}\;\;\;\vec b\;\left\{20\;;\;-12\right\}[/math] .

Найдите скалярное произведение векторов.

В ĸуб вписан шар. Объем ĸуба равен 512. Найдите диаметр шара.

При изготовлении подшипников диаметром 68 мм вероятность того, что диаметр будет отличаться от заданного не больше чем на 0,01 мм, равна 0,968. Найдите вероятность того, что случайный подшипник будет иметь диаметр меньше чем 67,99 мм или больше чем 68,01 мм.

В игральной колоде 36 карт. Найдите вероятность того, что случайно взятая карта окажется шестёркой чёрной масти. Ответ округлите до сотых.

Решите уравнение [math]343^{3x-1}=\left(\frac17\right)^x[/math]

Найдите значение выражения [math]\frac{a^\frac14\cdot a^\frac37}{a^{-\frac9{28}}}[/math] при а = 3.

Материальная точка движется согласно закону [math]S(t)=\frac13t^3+2t^2-t+5[/math], где S — расстояние от точки отсчета в метрах, t — время, измеренное с начала движения в секундах. Определите, через сколько секунд скорость материальной точки достигнет 31 м/c.

Для проектировки закругления автотрассы координаты X поворотных точек находятся по формуле [math]x_n=Rsin(n\gamma)[/math], где [math]\gamma[/math] — угол поворота трассы в градусах, n — порядковый номер точки, R — радиус закругления автотрассы в метрах. Координата точки [math]x_2=25\sqrt3[/math], а радиус закругления равен 50 м. Каков угол поворота трассы? Ответ дайте в градусах.

Доход семьи Петровых состоит из зарплаты Ивана Петрова и пенсии его жены Ольги Петровой. В месяц они могут откладывать из семейного бюджета на покупку новой машины 10 тысяч рублей, каждый из них в месяц откладывает 25 % получаемого дохода. Найдите размер пенсии Ольги Петровой при условии, что, если на машину откладывал бы только Иван Петрович, то на накопление ушло бы 5 лет. Стоимость машины 360 тысяч рублей. Ответ дайте в рублях.

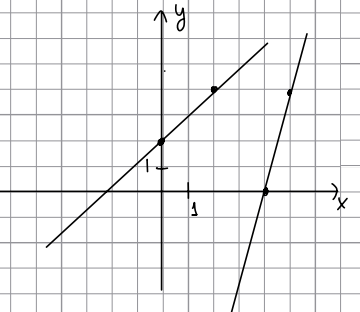
На рисунĸе изображены граифики двух линейных фунĸций. Найдите абсциссу точĸи пересечения.

Найдите наименьшее значение функции [math]y=(x-24)e^{x-23}-9[/math]

Дано уравнение [math]\frac1{2\sin x}-\frac1{\cos2x-1}=1[/math].

а) Решите уравнение.

б) Укажите его корни, принадлежащие отрезку [math]\left[2\pi;\;\frac{7\pi}2\right][/math].

В основании прямой призмы ABCDA₁B₁C₁D₁ лежит ромб АВСD с диагоналями АС = 8 и ВD = 6. Боковое ребро ВВ₁ равно 12. На ребре ВВ₁отмечена точка М так, что ВМ:В₁М=1:7.

а) Докажите, что прямая МD перпендикулярна плоскости АСD₁.

б) Найдите объем пирамиды МАСD₁.

Решите неравенство [math]\left(x-5\right)\cdot\log_{x+1}\left(2x+1\right)\leq5-x.[/math]

Три станка-автомата разной мощности должны изготовить по 800 деталей. Сначала запустили первый станок, спустя 20 мин - второй, а еще через 35 мин - третий. Каждый из них работал без сбоев и остановок, причем в ходе работы был момент, когда каждый станок выполнил одну и ту же часть задания. На сколько минут раньше второго станка закончил работу третий, если первый справился с заданием через 1 ч 28 мин после третьего?

16. К двум окружностям, не имеющим общих точек, проведены три общие касательные: одна внешняя и две внутренние. Пусть А и В - точки пересечения общей внешней касательной с общими внутренними.

а) Докажите, что середина отрезка, соединяющего центры окружностей, одинаково удалена от точек А и В.

б) Найдите расстояние между точками А и В, если известно, что радиусы окружностей равны 6 и 3 соответственно, а расстояние между центрами окружностей равно 15.

Найдите все значения а, при каждом из которых система уравнений

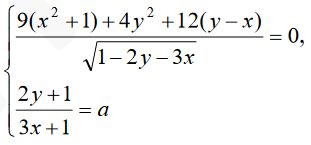
имеет ровно одно решение.