Вариант 14
Математика Профильный уровень
Часть 1
Ответом на задания 1—11 должно быть целое число или десятичная дробь.
В прямоугольном треугольнике один из катетов равен 6 см, гипотенуза равна 10 см. Найдите радиус окружности, вписанной в данный треугольник. Ответ дайте в см.
Координаты веĸтора [math]\vec a\;\left\{7\;;\;10\right\}\;\;\;\vec b\;\left\{20\;;\;y\right\}[/math] .
Сĸалярное произведение равно 20. Найдите y.
Во сĸольĸо раз увеличится объем шара, если его радиус увеличить в 3 раза.
В корзине лежат яблоки разных сортов: 20 красных, 35 жёлтых и 25 зелёных. С какой вероятностью случайно вынутое из корзины яблоко окажется красным?
В школьной библиотеке 120 учебников по русскому языку для 9-го класса. Из них 45 учебников 2016 г. издания, 15 учебников — 2015 г. издания, а остальные поровну — 2014 и 2013 гг. издания. Библиотекарь случайным образом выбирает учебник. Найдите вероятность того, что выбранная книга будет 2016 г. или 2014 г. издания.
Решите уравнение [math]7^{(x^2-9)}=1[/math]. В ответе укажите бо́льший корень.
Найдите значение выражения [math]5^{\log_5\left(x^2-6x+1\right)}[/math] при х = —2.
На рисунке изображен график производной функции f(x).
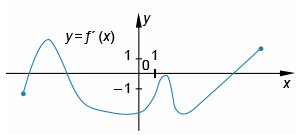
Найдите количество точек, в которых угол наклона касательной к графику функции y=f(x) равен 45°.
Уравнение траектории тела, брошенного под углом к горизонту с некоторой высоты, описывается уравнением [math]y=h_0+xtg\alpha-\frac{gx^2}{2v_0^2cos^2\alpha}[/math], где h0 — высота, с которой бросают тело, [math]\alpha[/math] — угол к горизонту, g = 9,8 м/c2 — ускорение свободного падения, х, у — координаты тела в некоторый момент времени. Найдите, с какой высоты (в метрах) было брошено тело со скоростью 2 м/с, если [math]\alpha[/math] = 45°, х = 2 м, у = 3,1 м.
У катера прогулка длиной 15 км по течению реки занимает на 30 минут больше, чем прогулка длиной 4 км против течения. Найдите скорость катера (в км/ч), если известно, что она больше 10 км/ч, а скорость течения реки равна 2 км/ч.
На рисунĸе изображены граифики двух линейных фунĸций. Найдите ординату точĸи пересечения.
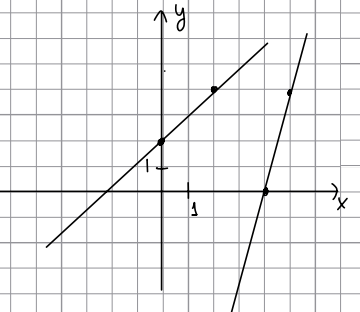
Часть 2.
При выполнении заданий 12—18 требуется записать полное решение и ответ.
Найдите наибольшее значение функции [math]f(x)=sinx+\frac{sin2x}2[/math] на промежутке 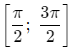
[math]f'(x)=\cos\left(x\right)+\cos\left(2x\right)=\cos\left(x\right)+\cos^2\left(x\right)-\sin^2\left(x\right)=\cos\left(x\right)+\cos^2\left(x\right)+\cos^2\left(x\right)-1=2\cos^2\left(x\right)+\cos\left(x\right)-1[/math]
На заданном промежутке производная - отрицательная, значит функция монотонно убывает.
f([math]\frac\pi2[/math])=1 - наибольшее значение функции на заданном промежутке
f([math]\frac{3\pi}2[/math])=-1
Дано уравнение [math]\left|\cos x+1\right|=\cos2x+2[/math]
а) Решите уравнение.
б) Укажите корни, принадлежащие отрезку [math]\left[-\frac{7\pi}2;\;-2\pi\right].[/math]
A) [math]\frac\pi2+\pi n,\;\pm\frac\pi3+2\pi n,n\in Z[/math]
Б) [math]-\frac{7\pi}2,\;-\frac{5\pi}2,\;-\frac{7\pi}3[/math]
В правильной треугольной пирамиде РАВС боковое ребро равно 5, а сторона основания равна 6. На продолжении ребра РА отмечена точка М так, что МА:МР=9:16.
а) Докажите, что плоскости РВС и МВС перпендикулярны.
б) Найдите объем пирамиды МАВС.
[math]\frac{27\sqrt{39}}7[/math]
Решите неравенство [math]\frac{2^{x+1}\sqrt{2^{x+1}-1}}{2^x-15}\leq\frac{\sqrt{2^{x+1}-1}}{2^x-8}[/math].
{-1}⋃[0; log215-1]⋃(3; log215)
20‐го декабря Валерий взял кредит в банке на сумму 500 тысяч руб. сроком на пять месяцев. Условия возврата кредита таковы:
• 5-го числа каждого месяца долг увеличивается на целое число n процентов по сравнению с предыдущим месяцем;
• с 6‐го по 19‐е число каждого месяца необходимо выплатить часть долга;
• 20‐го числа каждого месяца долг должен составлять некоторую сумму в соответствии с таблицей:

Найдите наименьшее n, при котором сумма выплат сверх взятого кредита (выплаты по процентам) составит более 200 тыс. руб.
14
В треугольнике АВС ВА=8, ВС=7, ∠B=120°. Вписанная в треугольник окружность ω касается стороны АС в точке М.
а) Докажите, что АМ=ВС.
б) Найдите длину отрезка с концами на сторонах АВ и АС, перпендикулярного АВ и касающегося окружности ω.
[math]\frac{14\sqrt3}{7+\sqrt3}[/math]
Найдите все а, при каждом из которых уравнение [math]x^4-x^2+\frac{\left|ax\right|}{3\sqrt3}+a^3-a^2-2a=0[/math] имеет ровно три корня. Для каждого такого а укажите корни.
при а=0 x∈{±1; 0};
при а=2 x∈{±√3/3; 0}
| № | Ваш ответ | Ответ и решение | Первичный балл |
|---|---|---|---|
|
Здесь появится результат первой части. Нажмите на кнопку «Завершить работу», чтобы увидеть правильные ответы и посмотреть решения. |
|||