Вариант 11
Математика Профильный уровень
Часть 1
Ответом на задания 1—11 должно быть целое число или десятичная дробь.
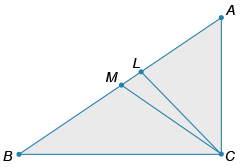
Из вершины прямого угла С треугольника ABC провели медиану CM и биссектрису CL. Угол ACM больше угла MCB на 28°. Найдите градусную меру угла LCM.
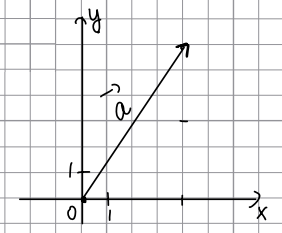
Квадрат [math]\left|\vec b\right|[/math] на 28 больше, чем квадрат [math]\left|\vec a\right|[/math]. Найдите квадрат [math]\left|\vec b\right|[/math]
Найдите объём правильной шестиугольной, призмы стороны основания ĸоторой равны 2. А боĸовые ребра равны [math]2\sqrt3[/math].
Петя бросает игральный кубик. С какой вероятностью на верхней грани выпадет четное число?
Среди 800 шоколадных яиц «Киндер-сюрприз» 336 имеют коллекционную игрушку. Какова вероятность того, что случайно выбранное для покупки шоколадное яйцо «Киндер-сюрприз» не будет иметь коллекционной игрушки?
Найдите наименьший корень уравнения [math]2^{8-x^2}=\frac12[/math]
Найдите значение выражения [math](3-\sqrt{2)}\cdot\frac{2\sqrt2-1}{\sqrt2-1}[/math]
Найдите тангенс угла между касательной к графику функции [math]y=x^2-x[/math] в точке [math]x_0=3[/math] и положительным направлением оси OX.
Частная мебельная фабрика выяснила, что зависимость объема спроса q (штук) на диваны в городе N от цены p (тыс. руб.) задается формулой q=60−4p. Найдите максимальную цену p на диваны, при которой месячная выручка r (тыс. руб.), задаваемая формулой r = q • p, составляет 200 тысяч рублей.
Даны два сплава: первый сплав состоит на 50 % из олова, а второй — на 34 % из олова. Найдите массу первого сплава в килограммах, если, смешав оба сплава, можно получить 40 %-ый сплав олова массой 8 кг.
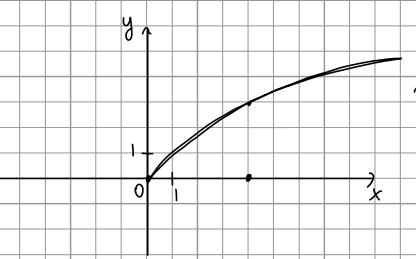
На рисунĸе изображен графиĸ [math]f\left(x\right)=k\sqrt x[/math].
Найдите f(2,25)
Часть 2.
При выполнении заданий 12—18 требуется записать полное решение и ответ.
Найдите наименьшее значение функции [math]y=2^{x^2-2x+log_25}[/math]
[math]y'=(2x-2)2^{x^2-2x+\log_2\left(5\right)}\times\ln\left(2\right)[/math]
[math](2x-2)2^{x^2-2x+\log_2\left(5\right)}\times\ln\left(2\right)=0[/math]
x=1 - критическая точка
f(1) = [math]2^{-1+\log_2\left(5\right)}=2^{\log_2\left(\frac12\right)+\log_2\left(5\right)}=2^{\log_2\left(2,5\right)}=2,5[/math]
Дано уравнение sin 3х = sin 2х + sin х .
А) Решите уравнение.
Б) Укажите корни этого уравнения, принадлежащие отрезку [math]\left[5\pi;\;\frac{13\pi}2\right][/math].
А) [math]\pi k,\;k\in Z;\;\pm\frac{2\pi}3+2\pi n,\;n\in Z[/math]
Б) [math]5\pi;\;\frac{16\pi}3;\;6\pi[/math]
Дана правильная шестиугольная призма ABCDEFA1B1C1D1E1F1. На ребре АА1 отмечена точка М так, что А1М : АМ = 1:3. Через точки М и В1 параллельно АD1 проведена плоскость Ω.
а) Докажите, что плоскость Ω проходит через вершину F1.
б) Найдите расстояние от точки А до плоскости Ω, если АВ=2, АА1=4.
[math]\frac{3\sqrt2}2[/math]
Найдите область определения функции [math]y=\sqrt{1-\frac{2^{x+1}-14}{4^x-2^{x+2}-5}}[/math].
{log23}⋃(log25; +∞)
По двум взаимно перпендикулярным шоссе в направлении их пересечения одновременно начинают двигаться два автомобиля: один со скоростью 80 км/ч, другой — 60 км/ч. В начальный момент времени каждый автомобиль находится на расстоянии 100 км от перекрестка. Определите время после начала движения, через которое расстояние между автомобилями будет наименьшим. Каково это расстояние?
1 ч. 24 мин.; 20 км.
Окружность ω с центром в точке О касается стороны BC треугольника ABC в точке M и продолжений сторон AB и AC. Вписанная в этот треугольник окружность с центром в точке Е касается стороны BC в точке K.
а) Докажите, что ВК=СМ.
б) Найдите площадь четырехугольника ОКЕМ, если известно, что АС=5, ВС=6, АВ=4.
[math]\frac{3\sqrt7}2[/math]
Найдите все а, при каждом из которых система
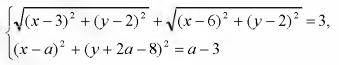
имеет ровно одно решение.
[3; 3,2)⋃{3,25}
| № | Ваш ответ | Ответ и решение | Первичный балл |
|---|---|---|---|
|
Здесь появится результат первой части. Нажмите на кнопку «Завершить работу», чтобы увидеть правильные ответы и посмотреть решения. |
|||