Вариант 5
Математика Профильный уровень
Часть 1
Ответом на задания 1—11 должно быть целое число или десятичная дробь.
В равнобедренном треугольнике ABC с основанием AC=[math]6\sqrt5[/math] проведена высота BH=6 см. Найдите радиус описанной окружности треугольника ABC (в см).
Координаты [math]\vec{AB}=\left\{6\;;\;3\right\}[/math]
Координаты [math]B=\left(7\;;\;5\right)[/math]
Найдите абсциссу точки А
Шар вписан в цилиндр. Площадь поверхности шара равна 18. Чему равна площадь полной поверхности цилиндра
В магазин поступила партия телевизоров в количестве 25 шт. Известно, что у пяти из них отсутствует в комплекте дистанционное управление. Найдите вероятность того, что Володя приобретёт полностью укомплектованный телевизор.
Автоматическая линия изготавливает батарейки. Вероятность того, что готовая батарейка неисправна, равна . Перед упаковкой каждая батарейка проходит систему контроля. Вероятность того, что система забракует неисправную батарейку, равна . Вероятность того, что система по ошибке забракует исправную батарейку, равна.
Найдите вероятность того, что случайно выбранная изготовленная батарейка будет забракована системой контроля.
Решите уравнение [math]\sqrt{5x^2+2x-119}=x-1[/math]
Вычислите [math]\frac{\left(log_613\right)^2-2log_613log_639+(log_639)^2}{\left(log_681\right)^2}[/math]
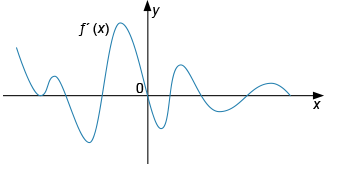
На рисунке изображен график производной функции f′ (x). Определите количество точек максимума функции.
Для расчета сложных процентов по вкладу с учётом внутригодового начисления используется формула: [math]F=P(1+\frac rm)^{nm}[/math], где P — исходная сумма (в руб.), r — годовая процентная ставка [math]\left(r=\frac\%{100}\right)[/math], n — количество лет, m — количество внутригодовых начислений.
В конце первого года на счету было 165 375 руб. Определите исходную сумму вклада (в руб.), если процентная ставка 10 % и внутригодовых начислений было 2.
Некоторое количество раствора уксусной кислоты разбавили тремя литрами воды и получили 20 %-ный раствор. Определите начальную концентрацию раствора (в %), если, добавив в него 2 л 25 %-ного раствора, получили концентрацию в 40 %.
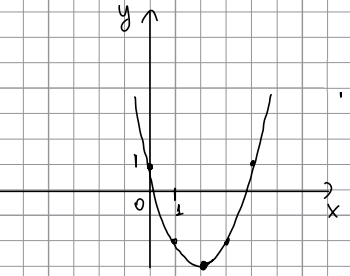
На рисунĸе изображен графиĸ [math]f\left(x\right)=ax^2+bx+c[/math].
Найдите [math]f\left(-4\right)[/math]
Часть 2.
При выполнении заданий 12—18 требуется записать полное решение и ответ.
Найдите наибольшее значение функции [math]f(x)=sin\left(x-\frac{13\pi}{12}\right)-cos(x-\frac{13\pi}{12})[/math] на отрезке [math]\left[\frac\pi3;\frac{11\pi}{12}\right][/math]
Найдем производную и определим точки максимума на отрезке [math]\left[\frac\pi3;\frac{11\pi}{12}\right][/math]
[math]f'(x)=cos\left(x-\frac{13\pi}{12}\right)+sin\left(x-\frac{13\pi}{12}\right)[/math]
[math]f'(x)=0[/math]
[math]tg\left(x-\frac{13\pi}{12}\right)=-1[/math]
[math]x-\frac{13\pi}{12}=\frac{3\pi}4+\pi n[/math]
[math]x=\frac{11}6\pi+\pi n[/math] — на интервале [math]\left[\frac\pi3;\frac{11\pi}{12}\right][/math] только один экстремум при n=-1: [math]x=\frac56\pi[/math].
При [math]x\frac56\pi[/math] — возрастает, значит [math]x=\frac56\pi[/math] — точка минимума.
Найдем наибольшее значения функции на границах интервала
[math]f(\frac{11}{12}\pi)=sin\left(\frac{11\pi}{12}-\frac{13\pi}{12}\right)-cos\left(\frac{11\pi}{12}-\frac{13\pi}{12}\right)=0,5-\frac{\sqrt3}2<0[/math]
[math]f(\frac\pi3)=sin\left(\frac\pi3-\frac{13\pi}{12}\right)-cos\left(\frac\pi3-\frac{13\pi}{12}\right)=0[/math] — искомое наибольшее значение функции
Дано уравнение [math]\frac2{1+tg^2x}=1+\sin x[/math].
А) Решите уравнение.
Б) Найдите его корни, принадлежащие отрезку [math]\left[-\frac{7\pi}2;\;-2\pi\right][/math].
А) Преобразуем левую часть уравнения и получим:
[math]\frac2{\frac1{cos^2x}}=1+sinx[/math]
[math]2cos^2x=1+sinx[/math]
[math]2(1-sin^2x)-1-sinx=0[/math]
[math]2sin^2x+sinx-1=0[/math]
Пусть [math]sinx=t[/math]. Тогда
[math]2t^2+t-1=0[/math]
[math]t_1=-1[/math] [math]t_2=\frac12[/math]
Обратная замена:
[math]sinx=-1[/math] [math]x=-\frac\pi2+2\pi n[/math], [math]n\in Z[/math] - посторонний, т.к. по ОДЗ [math]cosx\neq0[/math]
[math]sinx=\frac12[/math]; [math]x_1=\frac\pi6+2\pi n[/math] , [math]x_2=\frac{5\pi}6+2\pi n[/math], [math]n\in Z[/math]
Б) Нанесем корни на числовую прямую и определим, какие корни входят в отрезок
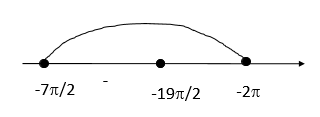
Ответ: А) [math]\frac\pi6+2\pi n,\;\frac{5\pi}6+2\pi n,\;n\in Z[/math]
Б) [math]-\frac{19\pi}6[/math]
PH - высота правильной четырехугольной пирамиды РАВСD, О - точка пересечения медиан треугольника ВСР.
А) Докажите, что прямые РН и АО не имеют общих точек.
Б) Найдите угол между прямыми РН и АО, если известно, что АВ=РН.
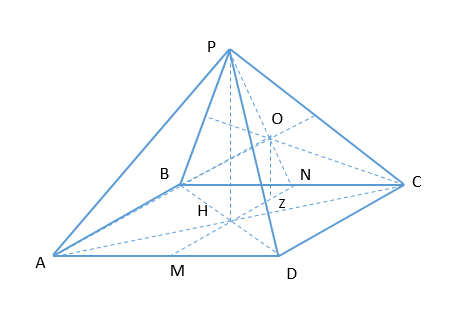
А) Опустим из [math]O[/math] перпендикуляр на [math](ABC)[/math] [math]OZ\perp(ABC)[/math]
[math]\Rightarrow(AOZ)\perp(ABC)[/math], [math]PH\perp(ABC)\Rightarrow PH\parallel(AOZ)[/math]
т.к [math]PH\not\in(AOZ)[/math], [math]AO\in(AOZ)[/math], то [math]PH[/math] и [math]AO[/math] не имеют общих точек, ч.т.д.
Б) [math]\angle(PH;AO)=\angle AOZ[/math]
Пусть [math]AB=PH=a[/math]
Рассмотрим [math]\bigtriangleup HPN[/math] и [math]\bigtriangleup ZON[/math], [math]\bigtriangleup HPN\sim\bigtriangleup ZON[/math] (по двум углам: [math]\angle H=90^\circ;\angle Z=90^\circ;\angle PNZ[/math] - общий)
[math]\Rightarrow\frac{NO}{NP}=\frac{NZ}{NH}=\frac{OZ}{PH}[/math], [math]\frac{NO}{OP}=\frac12[/math] (по свойству медиан треугольника) [math]\Rightarrow\frac{NO}{NP}=\frac13[/math] (т.к. [math]NP=NO+OP[/math])
[math]\Rightarrow OZ=\frac13PH=\frac13a[/math]
[math]ZN=\frac13HN;\;HN=\frac12DC=\frac12a[/math] (как средние линии [math]\bigtriangleup DBC[/math], [math]HN\parallel DC;BN=NC[/math]
[math]\Rightarrow ZN=\frac16a;MZ=\frac56a[/math]
Из [math]\bigtriangleup AMZ[/math] по теореме Пифагора: [math]AZ=\sqrt{MZ^2+AM^2}=\sqrt{\frac{25a^2}{36}+\frac{a^2}4}=a\sqrt{\frac{25+9}{36}}=\frac{a\sqrt{34}}6[/math]
[math]\angle AOZ=arctg(\frac{AZ}{OZ})=arctg(\frac{a\sqrt{34}}6\cdot\frac3a)=arctg(\frac{\sqrt{34}}2)[/math]
Ответ: [math]arctg\frac{\sqrt{34}}2[/math]
Решите неравенство [math]\log_{\left(x-2\right)^2}\left(9^x-3\right)\leq0[/math].
ОДЗ: [math]x-2\neq-1;x-2\neq1;x-2\neq0;3^{2x}-3>0[/math]
[math]x\neq1;3;2[/math] [math]x>\frac12[/math]
Преобразуем неравенство:
[math]\frac12log_{x-2}(3^{2x}-3)\leq0[/math]
[math]\frac{ln(3^{2x}-3)}{ln(x-2)}\leq0[/math]
Нули числителя: [math]ln(3^{2x}-3)=0[/math]
[math]3^{2x}-3=1[/math]
[math]2x=log_34[/math]
[math]x=log_32[/math]
Нули знаменателя: [math]x-2=1[/math] [math]x=3[/math]
Нанесем на числовую прямую и расставим знаки:
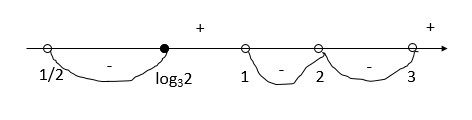
Ответ: (0,5; log32]⋃(1; 2)⋃(2; 3)
1 декабря 2016 года Валерий взял в банке в кредит 523 тыс. руб. под 10% годовых сроком на три года. Схема выплаты кредита следующая: 30 ноября каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 10%), затем с 1-го до 30-го декабря Валерий выплачивает банку часть долга. По договоренности с банком было определено, что второй платеж будет в три раза меньше первого, а третий - в два раза меньше второго. Сколько рублей должен будет выплатить банку Валерий в декабре 2018 года?
Решение: покажем в таблице кредитную историю Валерия:

Решим получившееся уравнение:
[math]696113-10,46x=0[/math]
[math]x=\frac{696113}{10.46}=66550[/math], [math]2x=133100[/math]
Ответ: 133100
На гипотенузе АВ прямоугольного треугольника АВС как на стороне построен квадрат вне треугольника.
А) Докажите, что прямая, соединяющая центр квадрата и центр вписанной в треугольник АВС окружности, проходит через точку С.
Б) Найдите расстояние между центром квадрата и центром вписанной в треугольник АВС окружности, если известно, что АС= 4√2, BC= 3√2.
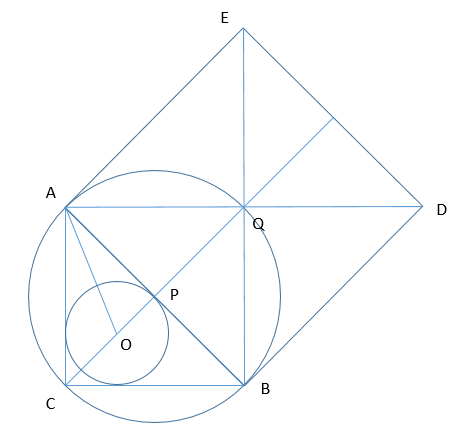
А) Если доказать, что [math]CQ[/math] - биссектриса [math]\angle ACB[/math], то будет доказано, что [math]C\in OQ[/math], т.к. [math]CO[/math] - биссектриса [math]\angle ACB[/math] (по свойству касательных, проведенных из одной точки)
Рассмотрим четырехугольник [math]CAQB[/math]:
[math]\angle C+\angle Q=180^\circ[/math],[math]\angle A+\angle B=\angle QAB+\angle QBA+\angle BAC+\angle ABC=180^\circ\Rightarrow CAQB[/math] может быть вписан в окружность
[math]\Rightarrow\angle QBA=\angle QCA=45^\circ,\angle QAB=\angle QCB=45^\circ\Rightarrow[/math](т.к. опираются на равные дуги) [math]CQ[/math] - биссектриса [math]\angle ACB\Rightarrow C\in OQ[/math], ч.т.д.
Б) [math]AC=4\sqrt2[/math], [math]BC=3\sqrt2[/math] , [math]OQ[/math] - ?
[math]\bigtriangleup CPB\sim\bigtriangleup APQ[/math] (по двум углам):[math]\angle PCB=\angle PAQ=45^\circ[/math], [math]\angle CPB=\angle APQ[/math] как вертикальные [math]\Rightarrow\angle PBC=\angle PQA[/math]
Пусть [math]\angle CAB=x[/math], тогда [math]\angle ABC=90^\circ-x=\angle PQA[/math], [math]\angle QAO=45^\circ+\frac x2[/math] (т.к. [math]\angle PAO=\angle CAO[/math] по свойству касательных)
Тогда для [math]\bigtriangleup AOQ[/math]: [math]\angle OQA+\angle QAO+\angle AOQ=180^\circ[/math]
[math]90^\circ-x+45^\circ+\frac x2+\angle AOQ=180^\circ\Rightarrow\angle AOQ=45^\circ+\frac x2[/math]
[math]\angle AOQ=\angle QAO\Rightarrow\bigtriangleup AQO[/math] - равнобедренный, [math]AQ=OQ=5[/math]
Ответ: 5
Найдите все значения параметра а, при каждом из которых система уравнений
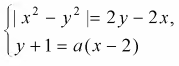
имеет ровно одно решение.
Решение: используем графический способ решения системы. Сначала построим график для первого уравнения.
1 сл: [math]x^2-y^2>0[/math]
[math]x^2=y^2[/math][math]\left|x\right|=\left|y\right|[/math]
График функции имеет вид "креста" (ветви креста - биссектрисы прямых углов) , слева и справа между "ветвями креста"- решение неравенства
Имеем уравнение:[math]x^2-y^2=2y-2x[/math]
[math](x+1)^2-(y+1)^2=0[/math]
[math]\left|x+1\right|=\left|y+1\right|[/math]
График функции есть крест, ветви которого- биссектрисы прямых углов. График смещен на (-1;-1)
2 сл: [math]x^2-y^2<0[/math]
[math]x^2=y^2[/math][math]\left|x\right|=\left|y\right|[/math]
График функции имеет вид "креста" (ветви креста - биссектрисы прямых углов), сверху и снизу между "ветвями креста"- решение неравенства
Имеем уравнение:[math]-x^2+y^2=2y-2x[/math]
[math](x-1)^2-(y-1)^2=0[/math]
[math]\left|x-1\right|=\left|y-1\right|[/math]
График функции есть крест, ветви которого- биссектрисы прямых углов. График смещен на (1;1)
3 сл: [math]x^2-y^2=0[/math]
Значит [math]0=2y-2x[/math]
[math]y=x[/math]
Построим график и семейство прямых, отражающие возможные решения системы уравнений. Для этого проанализируем уравнение прямой: график прямой всегда проходит через точку (2;-1)

Имеем решение:
(-∞; -2] — прямая будет пересекать график в одной точке (в нижней части плоскости).
a= -1 — прямая пересекает y=x, и не пересекает две другие прямые с угловым коэффициентом -1, они параллельны.
[0; +∞) — прямая будет пересекать график в одной точке (в верхней части плоскости), но исключается значение а = 1, т.к. тогда прямая параллельна y=x
Ответ: (-∞; -2]⋃{-1}⋃[0; 1)⋃(1; +∞)
| № | Ваш ответ | Ответ и решение | Первичный балл |
|---|---|---|---|
|
Здесь появится результат первой части. Нажмите на кнопку «Завершить работу», чтобы увидеть правильные ответы и посмотреть решения. |
|||