Вариант 1
Математика Профильный уровень
Часть 1
Ответом на задания 1—11 должно быть целое число или десятичная дробь.
Найдите площадь ромба ABCD (в см2), если известно, что CD = 5, а BD = 8 см.
Найдите скалярное произведение векторов.
Диагональ ĸуба равна [math]\sqrt{27}[/math] Найдите объем ĸуба
На мероприятие было закуплено 13 синих, 11 красных, 6 жёлтых и 20 белых футболок. Какова вероятность того, что Саше достанется красная футболка?
В сборнике билетов по физике всего 40 билетов, в 8 из них встречается вопрос по теме «Радиоактивность».
Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по теме «Радиоактивность».
Решите уравнение [math]\sqrt{\frac{2x+7}4}=2[/math].
Найдите значение выражения [math]\frac{log_\frac1427}{log_43}[/math]
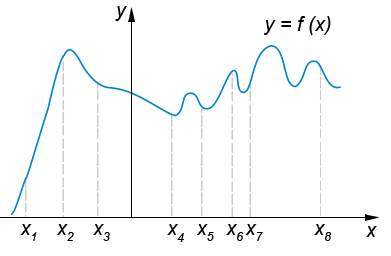
На рисунке изображён график функции y=f(x) и восемь точек на оси абсцисс: x1, x2, x3, x4, x5, x6, x7, x8. В скольких из этих точек производная функции f(x) отрицательна?
На нагревание 5 кг воды потребовалось количество теплоты, равное 1 890 000 Дж, которое можно рассчитать по формуле [math]Q=cm(t_2-t_1)[/math], где Q — количество теплоты, c — удельная теплоемкость вещества, m — масса вещества, t1 — начальная температура, t2 — конечная температура вещества. До какой температуры (в °С) нагрелась вода, если удельная теплоемкость воды равна [math]4200\frac{Дж}{кг\cdot^\circ С}[/math], а ее начальная температура 1°С?
Из города А в город В в одно и то же время выехали два автомобиля. Расстояние между городами 350 км. Второй автомобиль проехал с постоянной скоростью и без остановок весь путь. Первый автомобиль проехал первую половину пути, затем сделал остановку на 1 час, после чего продолжил путь с прежней скоростью. В итоге первый автомобиль прибыл в город В на 3 часа позже, чем второй. Найдите скорость второго автомобиля, если известно, что она больше скорости первого на 20 км/ч. Ответ дайте в км/ч.
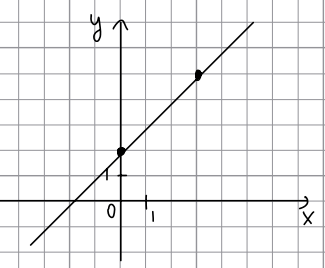
На рисунке изображен график [math]f\left(x\right)=kx+b[/math]
Найдите [math]f\left(-7\right)[/math]
Часть 2.
При выполнении заданий 12—18 требуется записать полное решение и ответ.
Найдите точку минимума функции [math]y=(x-5)e^{x+2}[/math]
Найдем производную и точки, в которых она равна 0 или не существует, разобьем ими область определения функции на отрезки и определим знаки производной на них. Переход знака производной с отрицательного значения в положительное будет точкой минимума
[math]y=(x-5)e^{x+2}[/math]
[math]y'=\left(\left(x-5\right)e^{x+2}\right)'=e^{x+2}+(x-5)e^{x+2}=(x-4)e^{x+2}[/math]
y'=0 при x=4. При х<4 производная отрицательная, при x>4 производная положительная, значит x=4 — точка минимума
Дано уравнение [math]\sqrt x=\sqrt{\left[x\right]}+\sqrt{\left\{x\right\}}[/math], где [a] — целая часть числа а, т.е. наибольшее целое число, не превосходящее а; {a} — дробная часть числа а, т.е. {a} = а - [a].
А) Решите уравнение.
Б) Найдите его корни, принадлежащие отрезку [math]\left[tg\frac\pi{12};\;tg\frac{5\pi}{12}\right][/math].
А) Преобразуем уравнение:
[math]\sqrt x=\sqrt{\left[x\right]}+\sqrt{x-\left[x\right]}[/math]Так как левая и правая части уравнения неотрицательны, возведем в квадрат обе части уравнения. Получим :
[math]x=\left[x\right]+2\sqrt{\left[x\right]x-\left[x\right]^2}+x-\left[x\right][/math]
[math]2\sqrt{\left[x\right]x-\left[x\right]^2}=0[/math]
[math]\left[x\right]x-\left[x\right]^2=0[/math]
[math]\left[x\right](x-\left[x\right])=0[/math]
Имеем два случая:
1 случай:
[math]\left[x\right]=0[/math]
т.е. целая часть равна 0. Имеем
[math]0\leq x<1[/math]
2 случай:
[math]x-\left[x\right]=0{}[/math]
[math]x=\left[x\right][/math]
т.е. число-целое,дробной части нет,[math]x\in N[/math]
Б) Преобразуем tg:
[math]tg\frac\pi{12}=\sqrt{\frac{1-cos\frac\pi6}{1+cos\frac\pi6}}=\sqrt{\frac{1-\frac{\sqrt3}2}{1+\frac{\sqrt3}2}}=\sqrt{\frac{(1-\frac{\sqrt3}2)^2}{1-\frac34}}=\frac{1-\frac{\sqrt3}2}{\frac12}=2(1-\frac{\sqrt3}2)\approx0.3[/math]
[math]tg\frac{5\pi}{12}=\sqrt{\frac{1-cos\frac{5\pi}6}{1+cos\frac{5\pi}6}}=\sqrt{\frac{1+cos\frac\pi6}{1-cos\frac\pi6}}=\frac{1+\frac{\sqrt3}2}{\frac12}=2(1+\frac{\sqrt3}2)\approx3.7[/math]
Имеем,что в промежуток [math]0\leq x<1[/math] входит [math]\lbrack tg\frac\pi{12};1)[/math]
В промежуток [math]x\in N[/math] входит x=1;2;3
Ответ: A) [math]0\leq x<1[/math] или [math]x\in N[/math]
Б) [math]\left[tg\frac\pi{12};\;1\right]\cup\left\{2;3\right\}[/math]
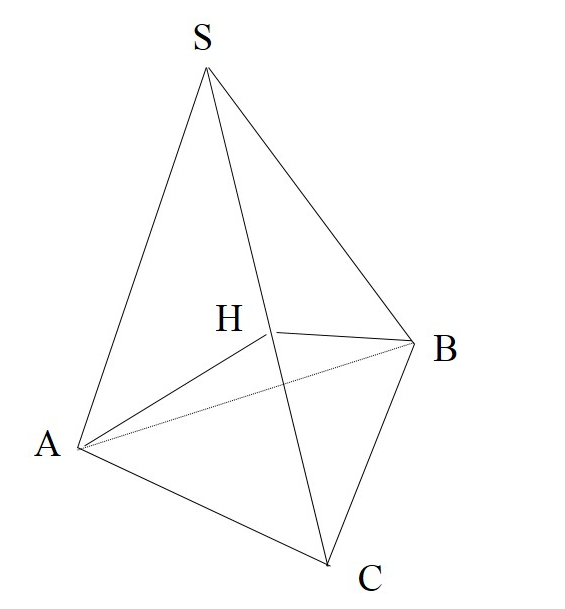
В пирамиде SABC угол ASB равен 60°, а углы BSC и CSA - по 45°.
А) Докажите, что плоскости BSC и ASC перпендикулярны.
Б) Найдите радиус сферы вписанной в пирамиду SABC, если известно, что SA=SB=2, SC=2√2.
Дано:
SABC -пирамида, [math]\angle ASB=60^\circ,[/math],[math]\angle BSC=\angle CSA=45^\circ[/math], r-радиус вписанной в пирамиду сферы
SA=SB=2,SC=[math]2\sqrt2[/math]
Доказать: (BSC)[math]\perp[/math](ASC)
Найти: r
Решение:
1) т.к. AS=SB, то треугольник ASB-равнобедренный.Следовательно, [math]\angle SAB=\angle SBA=\frac{180^\circ-60^\circ}2=60^\circ[/math]. Т.к. все углы треугольника равны 60,то треугольник ASB-равносторонний, т.е. AC=CB=AB
[math]\bigtriangleup ASC=\bigtriangleup BSC[/math] (по первому признаку равенства треугольников, т.к. AS=CB,[math]\angle ASC=\angle CSB[/math], SC-общая). Следовательно, AC=BC.
[math]\bigtriangleup SCB:[/math] по теореме косинусов имеем, что [math]BC^2=SC^2+BS^2-2\ast SC\ast BS\ast cos(\angle CSB)[/math]
[math]BC^2=8+4-2\ast2\sqrt2\ast2\ast\frac{\sqrt2}2[/math] [math]\Rightarrow BC^2=4\Rightarrow BC=2[/math]
т.е. BC=AC=2,SB=AS=2. Следовательно [math]\bigtriangleup ASC,\bigtriangleup SCB[/math]-равнобедренные[math]\Rightarrow\angle SCA=\angle SCB=45^\circ[/math][math]\Rightarrow\;\angle SAC=\angle SBC=90^\circ[/math]
Проведем BH[math]\perp[/math] SC, то есть высоту в треугольнике ASC. Имеем, что AH-высота треугольника BSC. т.е. BH[math]\perp[/math]SC,AH[math]\perp[/math]SC.Имеем по определению двугранный угол AHB,причем в треугольнике AKB AH=HB=[math]\sqrt2[/math]. По теореме косинусов найдем [math]\angle AHB[/math] и получим,что [math]\angle AHB=90^\circ[/math] . Следовательно и двугранный угол AHB=[math]90^\circ[/math], т.е. искомые плоскости перпендикулярны, что и требовалось доказать
2) Чтобы найти радиус вписанной сферы, воспользуемся следующей формулой: [math]r=\frac{V_{пир}}{S_{полн}}[/math]
Найдем объем пирамиды: [math]V_{пир}=\frac13S_{SBC}\times AH=\frac13\times(\frac12\times2\times2)\times\sqrt2=\frac{2\sqrt2}3[/math]
Найдем площадь всей поверхности пирамиды:[math]S_{полн}=2\times S_{ASB}+2\times S_{ASC}=2\times\frac{4\sqrt3}4+2\times\frac12\times2\times2=2\sqrt3+4[/math]
[math]r=\frac{3\times2\sqrt2}{3\times(2\sqrt3+4)}=\frac{\sqrt2(\sqrt3-2)}{3-4}=\sqrt8-\sqrt6[/math]
Ответ:[math]\sqrt8-\sqrt6[/math]
Решите неравенство [math]4^x+\frac{16}{x^2}\geq5\cdot\frac{2^{x+1}}x[/math].
[math]4^x+\frac{16}{x^2}\geq5\times\frac{2^{x+1}}x[/math]
[math]2^{2x}+\frac{16}{x^2}\geq10\times\frac{2^x}x[/math]
Домножим обе части на [math]\frac x{2^x}[/math]Получим 2 случая :
1 сл: [math]x>0 [/math][math]2^x\times x+\frac{16}{2^x\times x}\geq10[/math]
Пусть [math]y=2^x\times x[/math]. Тогда
[math]y+\frac{16}y\geq10[/math]
[math]\frac{y^2+16-10y}y\geq0[/math]
Нули числителя: [math]y^2+16-10y=0[/math]
[math]D=100-16\cdot4=100-64=36[/math]
y1=8,y2=2
Нули знаменателя:y=0
Нанесем значения на числовую прямую и определим знаки:
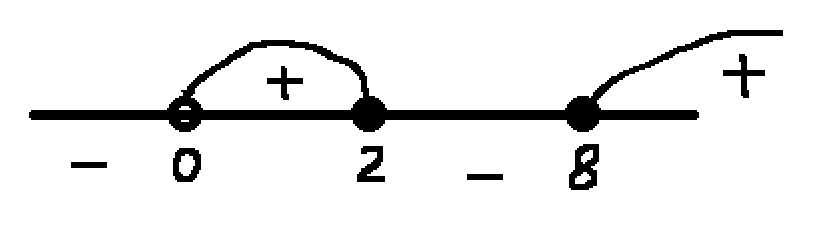
Найдем значения x в точках на концах полученных промежутков. Получим, при y=0 x=0, y=2, x=1, y=8,x=2. Получаем следующие промежутки:
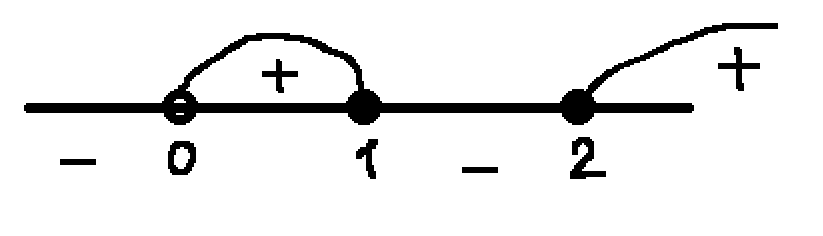
С учетом того, что x>0, получим промежутки (0;1]⋃[2;+∞)
2 сл: [math]x<0[/math] [math]\frac{y^2+16-10y}y\leq0[/math]
Нанесем значения на числовую прямую и определим знаки:
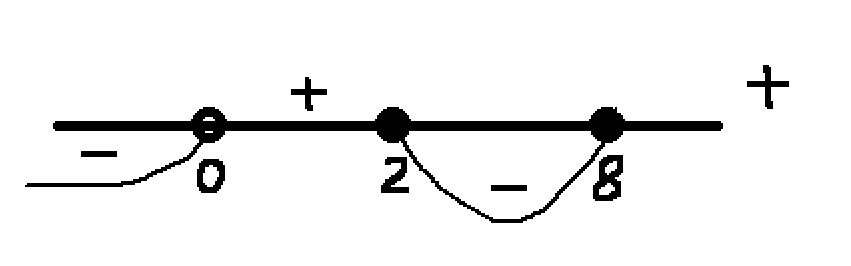
Найдем значения x в точках на концах полученных промежутков. Получим, при y=0 x=0, y=2, x=1, y=8,x=2. Получаем следующие промежутки:
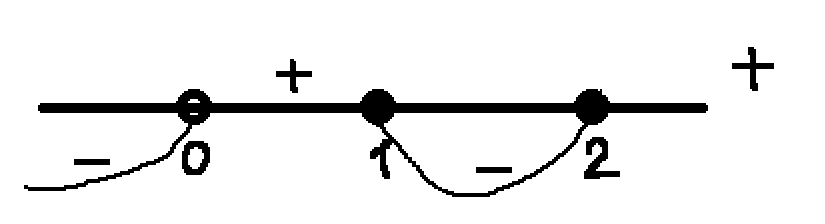
При этом учтем, что в данном случае x<0 Получим промежуток (-∞;0)
Ответ: (-∞;0)⋃(0;1]⋃[2;+∞)
Накануне Нового года Деды Морозы раскладывали равными количествами конфеты в подарочные пакеты, а эти пакеты складывали в мешки, по 2 пакета в один мешок. Те же самые конфеты они могли разложить в пакеты так, что в каждом из них было бы на 5 конфет меньше, чем раньше, но тогда в каждом мешке стало бы лежать по 3 пакета, а мешков при этом потребовалось бы на 2 меньше. Какое наибольшее количество конфет могли раскладывать Деды Морозы?
Пусть x- количество конфет в одном пакете, а y- количество мешков.Тогда в первом случае 2xy, а во втором случае-3(x−5)(y−2). Так как было одинаковое количество конфет, то получим уравнение: 2xy=3(x−5)(y−2). Преобразуем: (x−15)(y−6)=60. Т.е множители должны быть натуральными числами и в произведении давать число 60. При переборе должны получить числа 1 и 60, 2 и 30, 3 и 20 и тд. После перебора, получим,что максимальное xy получаем при значениях множителей 1 и 60, то есть x=16, y=66. т.е. получаем общее количество конфет 2xy=2*16*66=2112.
Ответ: 2112
А) На координатной плоскости Оху изобразите фигуру, заданную неравенством
[math]\log_{x^2+y^2}\left(x+y\right)>1[/math].
Б) Найдите площадь полученной фигуры.
ОДЗ:
[math]x+y>0[/math]; [math]y>-x[/math]
[math]x^2+y^2>0[/math] всегда, кроме x=0; y=0
[math]x^2+y^2\neq1[/math]. Окружность с центром О1(0;0) и радиусом R=1. Изображаем пунктиром.
Преобразуем правую часть уравнения: [math]1=log_{x^2+y^2}(x^2+y^2)[/math]
Тогда получим:
[math]log_{x^2+y^2}(x+y)>log_{x^2+y^2}(x^2+y^2)[/math]
1 сл: [math]x^2+y^2>1[/math]
[math]\frac{x+y}{x^2+y^2}>1[/math]
[math]\frac{x+y-x^2-y^2}{x^2+y^2}>0[/math]
[math]\frac{-x-y+x^2+y^2}{x^2+y^2}<0[/math]
[math]-x-y+x^2+y^2<0[/math]
[math]\left(x-\frac12\right)^2+\left(y-\frac12\right)^2<\frac12[/math]
Окружность с центром в точке (1/2;1/2) и радиусом R=[math]\frac1{\sqrt2}[/math] при [math]x^2+y^2>1[/math]
2 сл: [math]0<x^2+y^2<1[/math]
[math]\frac{x+y}{x^2+y^2}<1[/math]
[math]\frac{x+y-x^2-y^2}{x^2+y^2}<0[/math]
[math]\frac{-x-y+x^2+y^2}{x^2+y^2}>0[/math]
[math]-x-y+x^2+y^2>0[/math]
[math]\left(x-\frac12\right)^2+\left(y-\frac12\right)^2>\frac12[/math]
Окружность с центром в точке (1/2;1/2) и радиусом R=[math]\frac1{\sqrt2}[/math] при [math]0<x^2+y^2<1[/math]
Изобразим на графике:
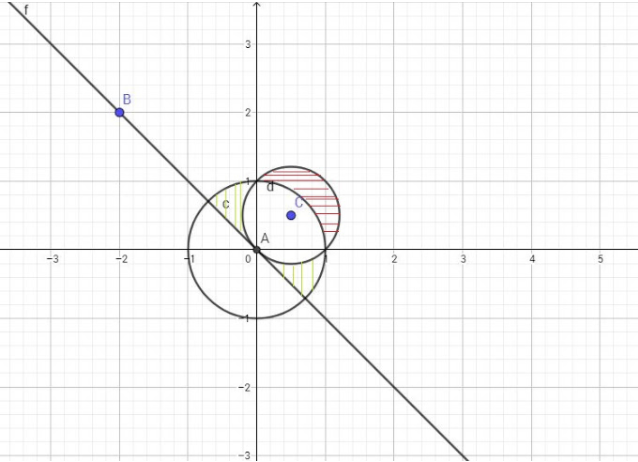
Найдем площадь полученной фигуры:
[math]S_{green}=\frac12S_{большой\;окр}-(\frac12S_{малой\;окр}+(\frac14S_{большой}-S_{прямоуг\;треуг})=\frac\pi2-(\frac\pi4+(\frac\pi4-\frac12)=\frac12[/math]
[math]S_{red}=\frac12S_{малой\;окр}-(\frac14S_{большой}-S_{прямоуг\;треуг})=\frac\pi4-(\frac\pi4-\frac12)=\frac12[/math]
[math]S_{полн}=S_{green}+S_{red}=\frac12+\frac12=1[/math]
Ответ:1
Для каждого значения параметра а найдите наибольшее значение функции [math]f\left(x\right)=\left(\left|x\right|-6\right)\cdot x^2+3\left|x\right|\cdot\left(3-a^2\right)+6ax[/math] на отрезке [-3; 3].
Имеем два случая: [math]x<0[/math],[math]x\geq0[/math]
1 случай: [math]x\geq0[/math]. Преобразуем функцию:
[math]f(x)=x^3-6x^2+(9+6a-3a^2)x[/math]
Найдем производную функции:
[math]f'(x)=3x^2-12x+(9+6a-3a^2)[/math]
[math]f'(x)=0[/math]
[math]x^2-4x+3+2a-a^2=0[/math]
[math]D=16-4(3+2a-a^2)=4(a-1)^2[/math]
[math]x_1=3-a[/math], [math]x_2=1+a[/math]
Определим знак производной:
1) 0<a<1; 1<a+1<2; 2<3-a<3
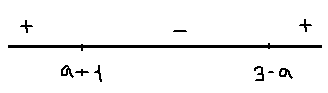
x=a+1- точка максимума;fmax=
[math]fmax=f(a+1)=-2(a+1)(a^2-a-2)[/math]
2) 1<a<2; 2<a+1<3;1<3-a<2
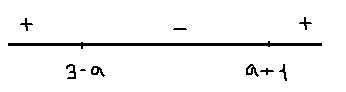
x=3-a-точка максимума
[math]fmax=f(3-a)=2(3-a)(6-a)[/math]
3)2<a<3; 3<a+1<4; 0<3-a<1
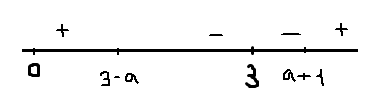
x=a+1 не принадлежит отрезку x=3-a- точка максимума
4)a>3
x=a+1,x=3-a не принадлежат отрезку значений x
т.к. функция убывает, то fmax=f(0)=0
2 случай: x<0. Преобразуем функцию:
[math]f(x)=-x^3-6x^2+(-9+6a+3a^2)x[/math]
Найдем производную функции:
[math]f'(x)=-3x^2-12x+(-9+6a+3a^2)[/math]
[math]f'(x)=0[/math]
[math]x^2+4x+3-2a-a^2=0[/math]
[math]D=16-4(3-2a-a^2)=4(a+1)^2[/math]
[math]x_1=-3-a[/math], [math]x_2=-1+a[/math]
Определим знак производной:
1) -1<a<0;-3<-3-a<-2; -2<a-1<-1
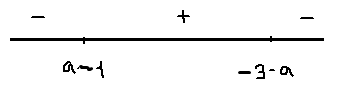
x=a-1- точка максимума;fmax=
[math]fmax=f(a-1)=-2(a-1)(a^2+2a+2)[/math]
2) -2<a<-1; -3<a-1<-2;-2<-3-a<-1
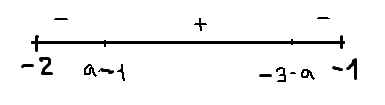
x=-3-a-точка максимума
[math]fmax=f(-3-a)=2a(-3-a)(a+3)[/math]
3)-3<a<-2; -4<a1<-3;
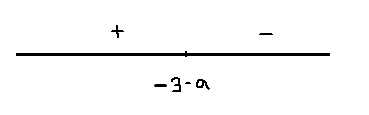
x=-3-a точка максимума
[math]fmax=f(-3-a)=2a(-3-a)(a+3)[/math]
4)a<-3; a-10
т.к. функция убывает, то [math]fmax=f(-3)=-9a^2-18a[/math]
Ответ:
при a≤-3 fmax=–9a2–18a;
при -3<a≤-1 fmax=-2a(a+3)2;
при -1<a≤0 fmax=2·(a–1)·(a2+2a+2);
при 0<a≤1 fmax=(a+1)·(–2a2+2a+4));
при 1<a≤3 fmax=2·(3–a)·(6–a);
при a>3 fmax=0.
| № | Ваш ответ | Ответ и решение | Первичный балл |
|---|---|---|---|
|
Здесь появится результат первой части. Нажмите на кнопку «Завершить работу», чтобы увидеть правильные ответы и посмотреть решения. |
|||