Демонстрационный вариант
Математика Профильный уровень
Часть 1
Ответом на задания 1—12 должно быть целое число или десятичная дробь.
Треугольник ABC вписан в окружность с центром O. Угол BAC равен 32°. Найдите угол BOC. Ответ дайте в градусах.
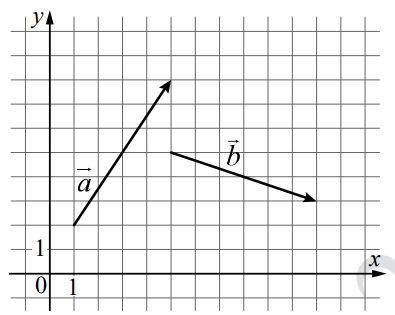
На координатной плоскости изображены векторы [math]\vec a\;и\;\vec b[/math]. Найдите скалярное произведение [math]\vec a\;\cdot\;\vec b[/math].
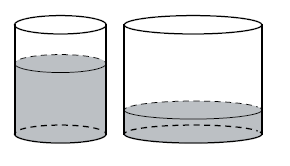
В первом цилиндрическом сосуде уровень жидкости достигает 16 см. Эту жидкость перелили во второй цилиндрический сосуд, диаметр основания которого в 2 раза больше диаметра основания первого. На какой высоте будет находиться уровень жидкости во втором сосуде? Ответ дайте в сантиметрах.
В сборнике билетов по биологии всего 25 билетов. Только в двух билетах встречается вопрос о грибах. На экзамене выпускнику достаётся один случайно выбранный билет из этого сборника. Найдите вероятность того, что в этом билете будет вопрос о грибах.
Симметричную игральную кость бросили 3 раза. Известно, что в сумме выпало 6 очков. Какова вероятность события «хотя бы раз выпало 3 очка»?
Найдите корень уравнения [math]3^{x-5}=81[/math]
Найдите sin 2α , если cos α=0,6 и π < α < 2π.
На рисунке изображён график дифференцируемой функции [math]y=f\left(x\right)[/math].
На оси абсцисс отмечены девять точек: x1 , x2 , ... x9 .
Найдите все отмеченные точки, в которых производная функции [math]f\left(x\right)[/math] отрицательна. В ответе укажите количество этих точек.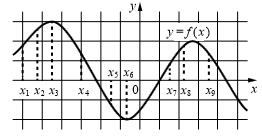
Локатор батискафа, равномерно погружающегося вертикально вниз, испускает ультразвуковой сигнал частотой 749 МГц. Приёмник регистрирует частоту сигнала, отражённого от дна океана. Скорость погружения батискафа (в м/с) и частоты связаны соотношением
[math]v=c\frac{f-f_0}{f+f_0}[/math]где c =1500 м/с – скорость звука в воде, [math]f_0[/math] – частота испускаемого сигнала (в МГц), [math]f[/math] – частота отражённого сигнала (в МГц). Найдите частоту отражённого сигнала (в МГц), если батискаф погружается со скоростью 2 м/с.
Весной катер идёт против течения реки в [math]1\frac23[/math] раза медленнее, чем по течению. Летом течение становится на 1 км/ч медленнее. Поэтому летом катер идёт против течения в [math]1\frac12[/math] раза медленнее, чем по течению. Найдите скорость течения весной (в км/ч).
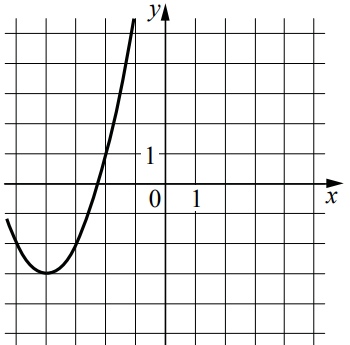
На рисунке изображён график функции вида [math]f\left(x\right)=ax^2+bx+c[/math] , где числа a , b и c — целые. Найдите значение [math]f\left(-12\right)[/math].
Найдите наименьшее значение функции
[math]y=9x-9ln\left(x+11\right)+7[/math][math]y=9x-9ln\left(x+11\right)+7[/math]на отрезке [−10,5; 0].
Часть 2.
При выполнении заданий 13—19 требуется записать полное решение и ответ.
а) Решите уравнение
[math]2\sin\left(x+\frac\pi3\right)+\cos2x=\sqrt3\cos x+1[/math]б) Укажите корни этого уравнения, принадлежащие отрезку
[math]\left[-3\pi;-\frac{3\pi}2\right][/math]а) Запишем исходное уравнение в виде:
[math]\sin x+\sqrt3\cos x+1-2\sin^2x=\sqrt3\cos x+1;{}\\\sin x-2\sin^2x=0;{}\\\sin x\cdot(2\sin^2x-1)=0[/math]Значит, [math]\sin x=0[/math], откуда [math]x=\pi k,\;k\ni Z[/math], или [math]\sin x=\frac12[/math], откуда [math]x=\frac\pi6+2\pi n,\;n\in Z[/math] или [math]x=\frac{5\pi}6+2\pi m,\;m\in Z[/math].
б) С помощью числовой окружности отберём корни, принадлежащие отрезку [math]\left[-3\pi;-\frac{3\pi}2\right][/math]
Получим числа: [math]-3\pi;-2\pi;-\frac{11\pi}6[/math]
Ответ: a) [math]\pi k,\;k\in Z;\;\frac\pi6+2\pi n,\;n\in Z;[/math]
[math]\frac{5\pi}6+2\pi m,\;m\in Z;[/math]
b) [math]-3\pi;\;-2\pi;\;-\frac{11\pi}6.[/math]
В пирамиде ABCD рёбра DA, DB и DC попарно перпендикулярны, а AB BC AC [math]5\sqrt2[/math] .
а) Докажите, что BD=CD .
б) На рёбрах DA и DC отмечены точки M и N соответственно, причём DM:MA=DN:NC=2:3. Найдите площадь сечения MNB .
Решите неравенство
[math]\log_{11}\left(8x^2a+7\right)-\log_{11}\left(x^2+x+1\right)\geq\log_{11}\left(\frac x{x+5}+7\right)[/math]Правая часть неравенства определена при [math]x-\frac{35}8[/math]
Поскольку при любых значениях x выражение [math]8x^2+7[/math] принимает положительные значения, при [math]x-\frac{35}8[/math] неравенство принимает вид:
[math]\frac{8x^2+7}{x^2+x+1}\geq\frac{8x+35}{x+5};\;\frac{8x^3+40x^2+7x+35}{(x+5)(x^2+x+1)}\geq\frac{8x^3+43x^2+43x+35}{(x+5)(x^2+x+1)};{}\\\frac{3x^2+36x}{(x+5)(x^2+x+1)}\leq0;\;\frac{3x(x+12)}{(x+5)(x^2+x+1)}\leq0[/math]
откуда [math]x\leq-12;\;-5<x\leq0[/math]. Учитывая ограничения [math]x-\frac{35}8[/math], получаем: [math]x\leq-12;\;-\frac{35}8<x\leq0[/math],
Ответ: [math](-\infty;-12\rbrack\;;\;(-\frac{35}8;0\rbrack[/math],
В июле 2025 года планируется взять кредит на десять лет в размере 800 тыс. рублей. Условия его возврата таковы:
– каждый январь долг будет возрастать на r% по сравнению с концом предыдущего года (r – целое число);
– с февраля по июнь каждого года необходимо оплатить одним платежом часть долга;
– в июле 2026, 2027, 2028, 2029 и 2030 годов долг должен быть на какую-то одну и ту же величину меньше долга на июль предыдущего года;
– в июле 2030 года долг должен составить 200 тыс. рублей;
– в июле 2031, 2032, 2033, 2034 и 2035 годов долг должен быть на другую одну и ту же величину меньше долга на июль предыдущего года;
– к июлю 2035 года долг должен быть выплачен полностью.
Известно, что сумма всех платежей после полного погашения кредита будет равна 1480 тыс. рублей. Найдите r.
По условию долг (в тыс. рублей) по состоянию на июль должен уменьшаться следующим образом:
800; 680; 560; 440; 320; 200; 160; 120; 80; 40; 0.
Пусть [math]k=1+\frac r{100}[/math]. Тогда последовательность размеров долга (в тыс. рублей) по 100 состоянию на январь такова:
800k; 680k; 560k; 440k; 320k; 200k; 160k; 120k; 80k; 40k.
Следовательно, платежи (в тыс. рублей) должны быть следующими:
800k - 680; 680k - 560; 560k - 440; 440k - 320; 320k - 200;
200k - 160; 160k - 120; 120k - 80; 80k - 40; 40k.
Значит, сумма всех платежей (в тыс. рублей) будет составлять:
5(560k - 440) +5(120k - 80) = 3400k - 2600.
Получаем: 3400k - 2600 =1480, откуда k = 1,2 и r = 20.
Ответ: 20.
Две окружности касаются внешним образом в точке K. Прямая AB касается первой окружности в точке A, а второй – в точке B. Прямая BK пересекает первую окружность в точке D, прямая AK пересекает вторую окружность в точке C./p>
а) Докажите, что прямые AD и BC параллельны./p>
б) Найдите площадь треугольника AKB, если известно, что радиусы окружностей равны 4 и 1.
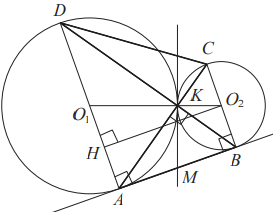
a) Обозначим центры окружностей [math]O_1\;и\;O_2[/math] соответственно. Пусть общая касательная, проведённая к окружностям в точке К, пересекает АВ в точке М. По свойству касательных, проведённых из одной точки, АM = KM и КМ = ВМ. Треугольник АКВ, у которого медиана равна половине стороны, к которой она проведена, прямоугольный.
Вписанный угол AKD прямой, поэтому он опирается на диаметр AD. Значит, AD [math]\perp[/math] AB. Аналогично получаем, что BC [math]\perp[/math] AB. Следовательно, прямые AD и ВС параллельны.
б) Пусть, для определённости, первая окружность имеет радиус 4, а вторая - радиус 1.
Треугольники BKC и AKD подобны, [math]\frac{AD}{BC}=4[/math]. Пусть [math]S_{BKS}=S[/math], тогда [math]S_{AKD}=16S[/math]
У треугольников AKD и AKB общая высота, следовательно, [math]\frac{S_{AKD}}{S_{AKB}}=\frac{DK}{KB}=\frac{AD}{BC}[/math], т.е. [math]S_{AKB}=4S[/math]. Аналогично [math]S_{CKD}=4S[/math]. Площадь трапеции ABCD равна 25S. Вычислим площадь трапеции ABCD. Проведём к AD перпендикуляр [math]O_2H[/math], равный высоте трапеции, и найдём его из прямоугольного треугольника [math]O_2HO_1[/math] :
[math]O_2H=\sqrt{O_1{O^2}_2-O_1H^2}=4[/math]
Тогда [math]S_{ABCD}=\frac{AD+BC}2\cdot AB=20[/math]
Следовательно, 25S = 20, откуда S = 0,8 и [math]S_{AKB}=4S=3.[/math]
Ответ: 3,2.
Найдите все положительные значения a , при каждом из которых система
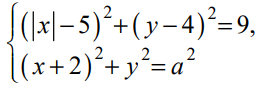
имеет единственное решение.
Если [math]x\geq0[/math], то уравнение [math]\left(\left|x\right|-5\right)^2+\left(y-4\right)^2=9[/math] задаёт окружность [math]\omega_1[/math] с центром в точке [math]C_1[/math](5; 4) радиусом 3, а если [math]x<0[/math], то оно задаёт окружность [math]\omega_2[/math] с центром в точке [math]C_2[/math](-5, 4) таким же радиусом (см. рисунок).
При положительных значениях а уравнение [math]\left(x+2\right)^2+y^2=a^2[/math] задаёт окружность [math]\omega[/math] с центром в точке С(-2; 0) радиусом а. Поэтому задача состоит в том, чтобы найти все значения а, при каждом из которых окружность [math]\omega[/math] имеет единственную общую точку с объединением окружностей [math]\omega_1\;и\;\omega_2[/math].
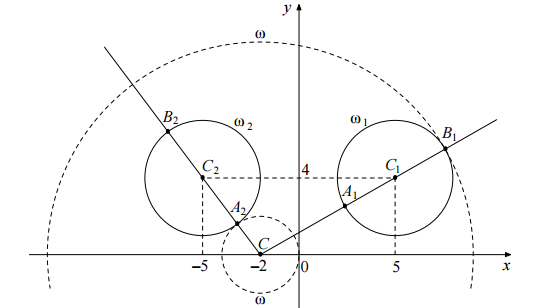
Из точки С проведём луч [math]CC_1[/math] и обозначим через [math]A_1[/math] и [math]B_1[/math] точки его пересечения с окружностью [math]\omega_1[/math], где [math]A_1[/math] лежит между С и [math]C_1[/math]. Так как
[math]CC_1=\sqrt{(5+2)^2\;+4^2}=65^2,\;то\;CA_1=\sqrt{65}\;-{},\;CB_1\;=\sqrt{65}+{}.[/math]
При [math]аСВ_1[/math], окружности [math]\omega\;и\;\omega_1[/math] не пересекаются.
При [math]СА_1<а<СВ_1[/math] окружности [math]\omega\;и\;\omega_1[/math] имеют две общие точки.
При [math]а=СА_1\;или\;а=СВ_1[/math], окружности [math]\omega\;и\;\omega_1[/math] касаются.
Из точки С проведём луч [math]CC_2[/math] и обозначим через [math]А_2\;и\;В_2[/math] точки его пересечения с окружностью [math]\omega_2[/math], где [math]A_2[/math] лежит между [math]С\;и\;С_2[/math]. Так как
[math]CC_2=\sqrt{(-5+2)^2+4^2}={},\;то\;CA_2=5-3={},\;CB_2=5+3={}.[/math]
При [math]аСВ_2[/math], окружности [math]\omega\;и\;\omega_2[/math], не пересекаются.
При [math]СА_2<а<\;СВ_2[/math] окружности [math]\omega\;и\;\omega_2[/math], имеют две общие точки.
При [math]а\;=СА_2\;или\;а=СВ_2[/math] окружности [math]\omega\;и\;\omega_2[/math], касаются.
Исходная система имеет единственное решение тогда и только тогда, когда окружность [math]\omega[/math] касается ровно одной из двух окружностей [math]\omega_1\;и\;\omega_2[/math] и не пересекается с другой. Так как [math]СА_2<СА_1<СВ_2<СВ_1[/math] , то условию задачи удовлетворяют только числа [math]а=2\;и\;а=\sqrt{65}+3[/math].
Ответ: [math]2\;;\;\sqrt{65}+3[/math]
Из пары натуральных чисел (a;b), где a >b , за один ход получают пару (a+b;a-b ).
а) Можно ли за несколько таких ходов получить из пары (100;1) пару, большее число в которой равно 400?
б) Можно ли за несколько таких ходов получить из пары (100;1) пару (806; 788)?
в) Какое наименьшее a может быть в паре (a;b), из которой за несколько ходов можно получить пару (806; 788)?
а) Из пары (100;1) за один ход получается пара (101; 99), за два хода получается пара (200; 2), за три хода получается пара (202;198), а за четыре хода получается пара (400; 4).
б) Заметим, что за один ход из пары (a;b) получается пара (а+b;а-b), а за два хода получается пара (2a; 2b). Следовательно, из пары (100;1) можно получить только пары [math]\left(2^k\cdot100;\;2^k\right)\;и\;\left(2^k\cdot101;\;2^k\cdot99\right)[/math], где k - неотрицательное целое число. Число 806 не равно [math]2^k\cdot100\;и\;2^k\cdot101[/math], а значит, пару (806; 788) невозможно получить за несколько ходов из пары (100;1).
b) Заметим, что пару (c;d) за один ход можно получить только из пары [math]\left(\frac{c+d}2;\frac{c-d}2\right)[/math] при условии, что числа с и d одной чётности.
Таким образом, пара (806; 788) получается из пары (797;9), которая получается из пары (403; 394). Пару (403; 394) невозможно получить за один ход ни из какой пары, поскольку числа 403 и 394 имеют разную чётность. Следовательно, наименьшее число а в паре (a;b), из которой занесколько ходов можно получить пару (806; 788), равно 403.
Ответ: а) да; б) нет; в) 403.
| № | Ваш ответ | Ответ и решение | Первичный балл |
|---|---|---|---|
|
Здесь появится результат первой части. Нажмите на кнопку «Завершить работу», чтобы увидеть правильные ответы и посмотреть решения. |
|||