Вариант 15

При покупке двух и более товаров в магазине предоставляется скидка 40 % на вещь, стоимость которой меньше, при условии, что изначальная стоимость всей покупки превышает 2000 руб. Сколько Маша заплатит за покупку, если юбка стоит 1600 руб., а свитер — 1800 руб.? Ответ дайте в рублях.

На графике изображено изменение температуры атмосферы на различной высоте над уровнем моря. По горизонтали указана высота над уровнем моря в километрах; по вертикали — температура атмосферы в градусах Цельсия. Для наглядности результаты измерений соединены линией.

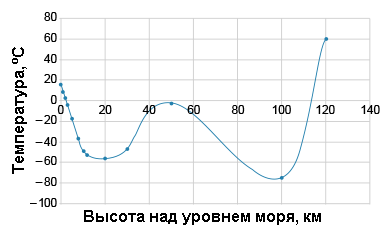
По графику определите, с какой высоты температура первый раз начинает возрастать.

Найдите тангенс угла ABC, если точки имеют следующие координаты: A(4;4), B(1;1), C(3;1)

В игральной колоде 36 карт. Найдите вероятность того, что случайно взятая карта окажется шестёркой чёрной масти. Ответ округлите до сотых.

Решите уравнение [math]343^{3x-1}=\left(\frac17\right)^x[/math]

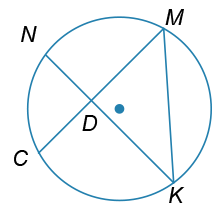
В окружности хорды NK и MC пересекаются под прямым углом в точке D. Найдите угол DKM (в градусах), если дуга KC, содержащая точки N и M, равна 260°.

Материальная точка движется согласно закону [math]S(t)=\frac13t^3+2t^2-t+5[/math], где S — расстояние от точки отсчета в метрах, t — время, измеренное с начала движения в секундах. Определите, через сколько секунд скорость материальной точки достигнет 31 м/c.

В шар вписан конус, радиус основания которого в 2 раза меньше радиуса шара. Найдите площадь поверхности шара (в см²), если длина окружности в основании конуса равна [math]6\sqrt\pi[/math] см.

Найдите значение выражения [math]\frac{a^\frac14\cdot a^\frac37}{a^{-\frac9{28}}}[/math] при а = 3.

Для проектировки закругления автотрассы координаты X поворотных точек находятся по формуле [math]x_n=Rsin(n\gamma)[/math], где [math]\gamma[/math] — угол поворота трассы в градусах, n — порядковый номер точки, R — радиус закругления автотрассы в метрах. Координата точки [math]x_2=25\sqrt3[/math], а радиус закругления равен 50 м. Каков угол поворота трассы? Ответ дайте в градусах.

Доход семьи Петровых состоит из зарплаты Ивана Петрова и пенсии его жены Ольги Петровой. В месяц они могут откладывать из семейного бюджета на покупку новой машины 10 тысяч рублей, каждый из них в месяц откладывает 25 % получаемого дохода. Найдите размер пенсии Ольги Петровой при условии, что, если на машину откладывал бы только Иван Петрович, то на накопление ушло бы 5 лет. Стоимость машины 360 тысяч рублей. Ответ дайте в рублях.

Найдите наименьшее значение функции [math]y=(x-24)e^{x-23}-9[/math]

Дано уравнение [math]\frac1{2\sin x}-\frac1{\cos2x-1}=1[/math].

а) Решите уравнение.

б) Укажите его корни, принадлежащие отрезку [math]\left[2\pi;\;\frac{7\pi}2\right][/math].

В основании прямой призмы ABCDA₁B₁C₁D₁ лежит ромб АВСD с диагоналями АС = 8 и ВD = 6. Боковое ребро ВВ₁ равно 12. На ребре ВВ₁отмечена точка М так, что ВМ:В₁М=1:7.

а) Докажите, что прямая МD перпендикулярна плоскости АСD₁.

б) Найдите объем пирамиды МАСD₁.

Решите неравенство [math]\left(x-5\right)\cdot\log_{x+1}\left(2x+1\right)\leq5-x.[/math]

16. К двум окружностям, не имеющим общих точек, проведены три общие касательные: одна внешняя и две внутренние. Пусть А и В - точки пересечения общей внешней касательной с общими внутренними.

а) Докажите, что середина отрезка, соединяющего центры окружностей, одинаково удалена от точек А и В.

б) Найдите расстояние между точками А и В, если известно, что радиусы окружностей равны 6 и 3 соответственно, а расстояние между центрами окружностей равно 15.

Три станка-автомата разной мощности должны изготовить по 800 деталей. Сначала запустили первый станок, спустя 20 мин - второй, а еще через 35 мин - третий. Каждый из них работал без сбоев и остановок, причем в ходе работы был момент, когда каждый станок выполнил одну и ту же часть задания. На сколько минут раньше второго станка закончил работу третий, если первый справился с заданием через 1 ч 28 мин после третьего?

Найдите все значения а, при каждом из которых система уравнений

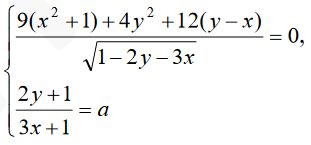
имеет ровно одно решение.

Может ли сумма четырех попарно различных дробей вида [math]\frac1n[/math] (где n∈N, n>1)

а) равняться 1,3;

б) равняться 1,001;

в) принимать значение из интервала [math]\left(\frac1{11};\;\frac1{10}\right)[/math]?