Вариант 13

Одна порция мороженого стоит 35 рублей 40 копеек. Кате нужно купить пять порций. Сколько сдачи Катя получит с 200 рублей (ответ укажите в рублях)?

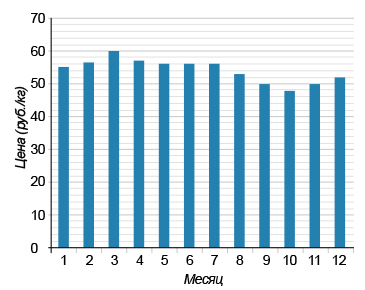
На диаграмме изображена динамика цен на сахар за 2017 год. По горизонтали указаны номера месяцев; по вертикали — цены за килограмм сахара в рублях. По диаграмме определите наибольшую цену сахара во втором полугодии 2017 года.

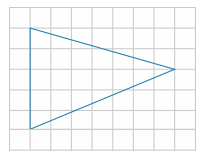
Найдите площадь треугольника, изображённого на клетчатой бумаге с размером клетки 1 см × 1 см. Ответ дайте в квадратных сантиметрах.

В коробке лежит стандартный комплект из 32 шахматных фигур. Найдите вероятность того, что случайно взятая из коробки фигура окажется слоном.

Решите уравнение [math](2x-1)^2=2x-4x^2[/math]. Если корней несколько, укажите меньший из них.

В равнобедренном треугольнике ABC с основанием AC высота BH и биссектриса AN пересекаются в точке О. Найдите угол BNA, если угол B равен 80°. Ответ дайте в градусах.

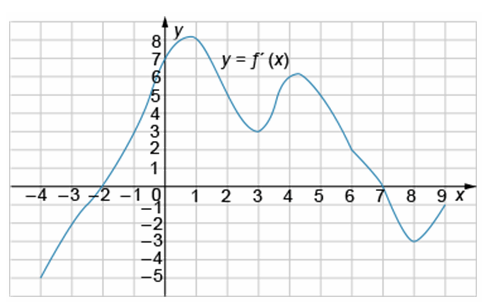
На рисунке представлен график производной функции y = f(x) на интервале [—4; 9]. Найдите точку минимума функции y = f(x) на данном промежутке.

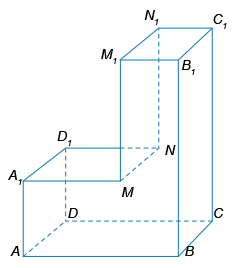
Найдите площадь поверхности фигуры, изображённой на рисунке, если CC₁ = 10, AB = 8 см, AA₁ = 4 см, A₁M = 5 см, BC = 3 см. Ответ дайте в квадратных сантиметрах.

Найдите значение выражения [math]\frac{\sqrt[5]{\sqrt{x^{24}}}}{\sqrt[10]{x^4}}[/math] при x = — 3.

Период свободных колебаний (в с) пружинного маятника определяется по формуле [math]T=2\pi\sqrt{\frac mk}[/math], где m — масса груза (в кг), k — жесткость пружины (в Н/м), [math]\pi=3[/math]. Груз какой массы (в кг) нужно закрепить на пружине жёсткостью 400 Н/м, чтобы период колебаний составил 0,9 с?

Два спортсмена отправились в велопробег длиной 108 км. Известно, что один из них двигался быстрее другого на 9 км/ч, но во время гонки его велосипед сломался и в течение 30 минут осуществлялся ремонт. После ремонта велосипедист продолжил движение и в результате прибыл на финиш на 30 минут раньше соперника. Определите, сколько часов потратил на преодоление всего пути велосипедист, прибывший на финиш вторым.

Найдите точку максимума функции y = 4•ln3x — 2x — 7.

Дано уравнение [math]\log_3^2\left(-tgx\right)-\log_3\sqrt{-tgx}=0[/math].

А) Решите уравнение.

Б) Укажите корни этого уравнения, принадлежащие интервалу [math]\left(4\pi;\;\frac{11\pi}2\right)[/math].

В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁ точка М лежит на ребре DD₁ так, что DM:D₁M=1:2. Плоскость, проходящая через точки А и М параллельно BD₁, пересекает ребро CD в точке Р.

а) Докажите, что CP=DP.

б) Найдите расстояние от точки D₁ до плоскости АМР, если известно, что АВ=12, ВС=9, АА₁=36.

Решите неравенство [math]\frac{4^x-3\cdot2^x+3}{2^x-2}+\frac{4^x-5\cdot2^x+3}{2^x-4}\leq2^{x+1}[/math].

Точка К лежит на диаметре АВ окружности с центром О. С и D - точки окружности, расположенные по одну сторону от АВ, причем ∠OCK = ∠ODK.

а) Докажите, что ∠CKB = ∠DKA.

б) Найдите площадь четырехугольника с вершинами в точках А, В, С, D, если известно, что OK = 3,6, BK = 9,6, ∠OCK = ∠ODK = 30°.

Два одинаковых бассейна одновременно начали наполняться водой. В первый бассейн поступает в час на 30 м³ больше воды, чем во второй. В некоторый момент в двух бассейнах вместе оказалось столько воды, сколько составляет объем каждого из них. После этого через 2 ч 40 мин наполнился первый бассейн, а еще через 3 ч 20 мин - второй. Сколько воды поступало в час во второй бассейн? За какое время наполнился второй бассейн?

Найдите все значения параметра а, при каждом из которых система уравнений

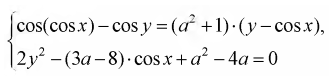
не имеет решений.

На доске записаны два натуральных числа: 672 и 560. За один ход разрешается любое из этих чисел заменить модулем их разности либо уменьшить вдвое (если число чётное).

а) Может ли через несколько ходов на доске оказаться два одинаковых числа?

б) Может ли через несколько ходов на доске оказаться число 2?

в) Найдите наименьшее натуральное число, которое может оказаться на доске в результате выполнения таких ходов.