Вариант 10

Вычислите значение выражения [math]2,5\cdot7,4+(8-5,4)\cdot2,5[/math]

Вычислите значение выражения [math]\frac{5^3\times6^{-6}}{3^2\times6^{-8}}[/math]

Незнайка выиграл приз в размере 600 000 рублей. Из этой суммы вычитается налог на доходы физических лиц в размере 13 %. Сколько рублей он получит после уплаты подоходного налога?

Найдите a из равенства F = ma, если F = 96 и m = 16.

Найдите значение [math]4^{log_418-log_23}[/math]

Плитка шоколада стоит 52 рубля 80 копеек. Какое наибольшее количество шоколадок можно купить на 300 рублей?

Найдите наименьший корень уравнения [math](2x+2)^2=(x+4)^2[/math]

Знайка перед покупкой изучил план квартиры: там было указано, что площадь прямоугольной прихожей равна 7,49 м². Но, измерив ширину и длину, он нашёл, что каждая из них равна 2,7 м. На сколько квадратных метров отличаются площади прихожей на плане и в реальности?

Установите соответствие между величиной (обозначено буквами) и её возможным значением (обозначено цифрами).

Величина

А) длина легкового автомобиля

Б) высота ступеньки

В) диаметр колеса легкового автомобиля

Г) толщина книги

Значение

1) 23 мм

2) 214 см

3) 7 дм

4) 15 см

Среди натуральных чисел от 23 до 37 случайно выбирают одно число. Найдите вероятность того, что оно не делится на 5.

На диаграмме показана средняя четвертная оценка лучших десяти учеников класса. Наибольшая средняя четвертная оценка у Красникова Владимира.

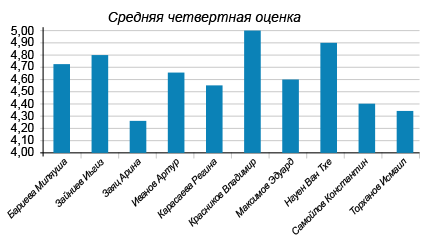
На каком месте в классе по средней четвертной оценке находится Торханов Исмаил?

Школьной столовой необходимо купить 250 литров сока у одного из трёх поставщиков. Цены и условия доставки приведены в таблице.

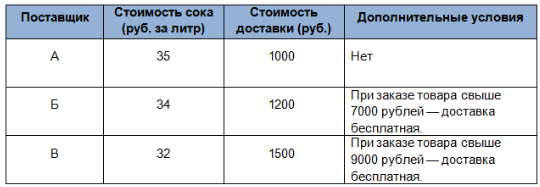
Сколько рублей необходимо заплатить за самую дешёвую покупку с доставкой?

Два бака одинакового объёма имеют цилиндрическую форму. Найдите диаметр основания первого бака, если известно, что диаметр основания второго бака равен 90 см, а уровень воды в первом баке в девять раза больше уровня воды во втором баке. Ответ запишите в сантиметрах.

На рисунке показано количество учащихся, записанных в городской центр творчества с сентября 2015 года по август 2016 года. По горизонтали указаны месяцы, по вертикали — количество учащихся (в чел.). Для наглядности точки соединены линиями.

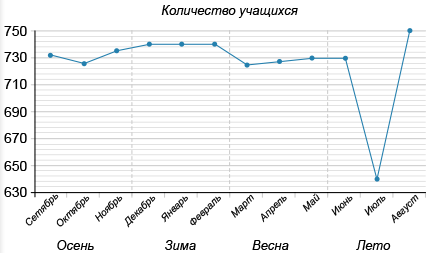
Пользуясь графиком, поставьте в соответствие каждому из указанных периодов (обозначено буквами) характеристику количества учащихся, записанных в городской центр творчества (обозначено цифрами).

Период

А) осень

Б) зима

В) весна

Г) лето

Характеристика

1) Количество учащихся не менялось.

2) Количество учащихся достигло наименьшего значения за весь год.

3) Количество учащихся ежемесячно увеличивалось.

4) Ежемесячное количество учащихся было больше 720, но меньше 738 человек.

В прямоугольный треугольник с катетами AB=3 см и BC=4 см вписана окружность. Найдите радиус этой окружности. Ответ запишите в сантиметрах.

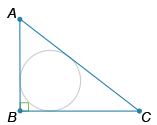
Найдите площадь S диагонального сечения куба с ребром, равным 5 см. В ответ запишите [math]S\sqrt2[/math] (см²).

На координатной прямой отмечены точки A, B, C, D.

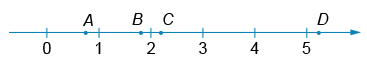
Установите соответствие между точкой (обозначено буквами) и соответствующим числом (обозначено цифрами).

Точка

А) A

Б) B

В) C

Г) D

Число

1) [math]\sqrt5[/math]

2) [math]4-\sqrt5[/math]

3) [math]log_3\sqrt5[/math]

4) [math]\frac4{3-\sqrt5}[/math]

В классе 22 учащихся. 15 из них были в Москве, 9 — в Санкт-Петербурге, также есть учащиеся, которые не были ни в Москве, ни в Санкт-Петербурге. Выберите 2 утверждения, которые верны при указанных условиях.

1) Если учащийся был в Санкт-Петербурге, то он обязательно был в Москве.

2) По крайней мере трое учащихся были и в Москве, и в Санкт-Петербурге.

3) В Москве не были 7 учащихся класса.

4) Ровно 12 учащихся были в Москве, но не были в Санкт-Петербурге.

Найдите наименьшее пятизначное натуральное число, которое записывается с помощью цифр 7 и 6 и делится на 12.

Внутри прямоугольного листа бумаги нарисован правильный пятиугольник. Через все стороны этого пятиугольника провели прямые так, что все они пересеклись внутри листа бумаги (не на краях листа). Сколько частей получится, если разрезать лист бумаги по всем проведенным прямым?