Вариант 2
Математика Базовый уровень
Ответом к каждому заданию является конечная десятичная дробь, целое число или последовательность цифр. Запишите ответы к заданиям в поле ответа справа от номера соответствующего задания. Если ответом является последовательность цифр, то запишите эту последовательность без пробелов, запятых и других дополнительных символов. Каждую цифру, знак «минус» и запятую пишите в отдельной клеточке в соответствии с приведёнными в бланке образцами. Единицы измерений писать не нужно.
Найдите значение выражения (0,89−0,17⋅4)⋅2.
Найдите значение выражения [math]\frac{14^2\cdot14^7}{\left(14^3\right)^3}[/math].
Из 28 человек, пришедших на родительское собрание, седьмая часть опоздала на 10 минут. Сколько родителей пришли вовремя?
Среднее квадратическое трёх чисел a, b и c вычисляется по формуле [math]d=\sqrt{\frac{a^2+b^2+c^2}3}[/math]. Найдите среднее квадратическое чисел [math]2\sqrt3[/math], [math]\sqrt{15}[/math] и [math]9[/math].
Найдите значение выражения [math]9^{\log_3\sqrt7}[/math].
Литр бензина на АЗС стоит 36,2 рубля. Сколько рублей сдачи должен получить Андрей с 1000 руб., если он заправляет свой автомобиль на 20 литров?
Найдите корень уравнения: 812x − 13=1.
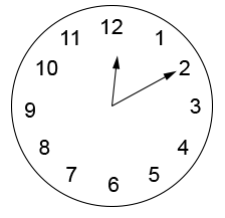
Какой угол (в градусах) образуют часовая и минутная стрелки в 12:10?
Установите соответствие между величиной (обозначено буквами) и её возможным значением (обозначено цифрами).
| ВЕЛИЧИНЫ | ВОЗМОЖНЫЕ ЗНАЧЕНИЯ |
| А) масса футбольного мяча | 1) 7,35 г |
| Б) масса шариковой ручки | 2) 55 кг |
| В) масса автомобиля | 3) 0,415 кг |
| Г) масса холодильника | 4) 2,5 т |
В коробке находятся 150 разноцветных воздушных шаров. Среди них 34 синих, 26 красных, 14 зеленых, 46 желтых, остальные — фиолетовые и белые, их поровну. Маша наугад достает из коробки один шар. Найдите вероятность того, что он будет не белым.
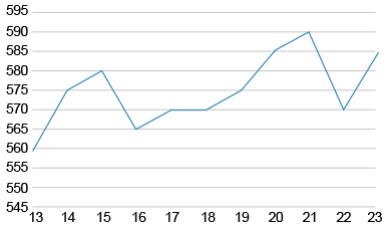
На рисунке изображен график изменения стоимости акций производственного предприятия с 13 по 23 октября 2016 года. По горизонтали указана дата, по вертикали – стоимость 1 акции в данный день (в руб.). Определите по графику разницу между наибольшей и наименьшей стоимостью 1 акции за представленный период.
В таблице указаны цены (в руб.) на услуги такси четырех разных фирм.
| Фирма такси | Посадка | Движение (за км) | Дополнительные условия |
| Экспресс | 100 | 20 | Нет |
| Тройка | 150 | 18 | Скидка 10% на поездки более 30 км |
| Эконом | 0 | 25 | Скидка 50% на каждый км после 20-го |
| Городское | 50 | 22 | Каждый км после 5-го — 20 руб. |
Определите, сколько рублей нужно заплатить за самую дешевую поездку длиной 30 км.
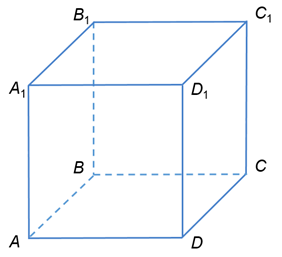
В кубе ABCDA1B1C1D1 провели сечение плоскостью, проходящей через вершины A1, C1 и D. Определите количество граней отсеченного многогранника ABCDA1B1C1.
На рисунке изображён график функции y=f(x). Точки a, b, c и d задают интервалы на оси Ox.
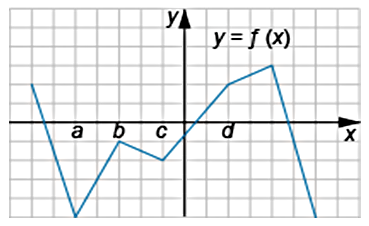
Пользуясь графиком, поставьте в соответствие каждому интервалу (обозначено буквами) характеристику функции и ее производной (обозначено цифрами).
| Интервал | Характеристика |
| А) (a; b) | 1) Значения производной функции отрицательны, значения функции отрицательны. |
| Б) (b; c) | 2) Значения производной функции положительны, значения функции отрицательны. |
| В) (a; c) | 3) Значения функции отрицательны. |
| Г) (c; d) | 4) Значения производной функции положительны. |
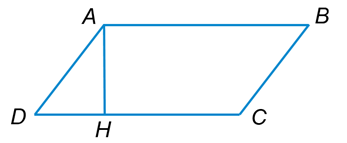
Площадь параллелограмма ABCD равна 48. AH — высота. Найдите длину отрезка HB, если AH=6.
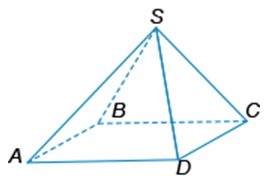
Объем правильной четырехугольной пирамиды SABCD равен 384 м3, а сторона её основания равна 12 м. Найдите длину апофемы данной пирамиды (в м).
На координатной прямой отмечены точки A, B, C и D.
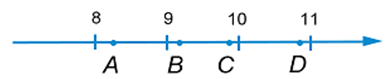
Каждой точке соответствует одно из чисел в правом столбце. Установите соответствие между указанными точками (обозначено буквами) и числами (обозначено цифрами).
| Точка | Число |
| А) А | 1) [math]\frac{150}{18}[/math] |
| Б) B | 2) [math]10-5^{-1}[/math] |
| В) C | 3) [math]\sqrt{85}[/math] |
| Г) D | 4) [math]6+\log_228[/math] |
В классе учатся 27 учеников. Известно, что бо́льшая часть из них сдала пробный ЕГЭ по математике на оценку "5" и никто из учеников не получил оценку "2". Выберите утверждения, которые верны при приведенных данных.
1) Оценку "5" получили менее 14 учеников.
2) Учеников, получивших оценку "3", меньше, чем получивших оценку "2".
3) В классе больше учеников, получивших "5", чем тех, кто написал работу на "3" или "4".
4) Найдутся 10 учеников, получивших за работу одинаковые оценки.
Приведите пример такого четырехзначного числа, кратного 5, но не кратного 10, произведение цифр которого равно 0, а сумма цифр равна числу, которое при делении на 7 и на 3 даёт равные ненулевые остатки.
На школьном турнире по старой системе подсчета очков за победу в шахматной партии игроку присуждается 1 очко, за ничью — 0,5 очка, за поражение — 0 очков. Известно, что на соревнованиях шахматист набрал 20 очков, сыграв 30 партий. Определите, сколько очков набрал бы этот шахматист, если бы на данных соревнованиях использовалась новая система подсчета очков: за победу — 1 очко, за ничью — 0 очков, за поражение — минус 1 очко (в случае поражения из набранных очков вычитается 1 очко).
| № | Ваш ответ | Ответ и решение | Первичный балл |
|---|---|---|---|
|
Здесь появится результат первой части. Нажмите на кнопку «Завершить работу», чтобы увидеть правильные ответы и посмотреть решения. |
|||