Вариант 3
Математика Профильный уровень
Часть 1
Ответом на задания 1—12 должно быть целое число или десятичная дробь.
При оплате услуг через платёжный терминал взимается комиссия 5%. Терминал принимает суммы, кратные 10 рублям. Пётр Агафонович хочет положить на счёт своего мобильного устройства не меньше 500 рублей. Какую минимальную сумму он должен положить в приёмное устройство данного терминала?
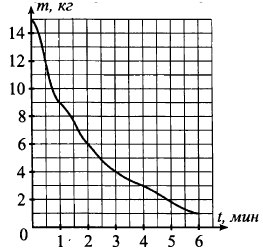
В ходе химической реакции количество исходного вещества (реагента), которое ещё не вступило в реакцию, со временем постепенно уменьшается. На рисунке 105 эта зависимость представлена графиком. На оси абсцисс откладывается время в минутах, прошедшее с момента начала реакции, на оси ординат — масса оставшегося реагента, который ещё не вступил в реакцию (в килограммах). Определите по графику, сколько килограммов реагента вступило в реакцию за первые четыре минуты.
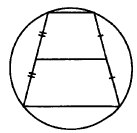
Около трапеции описана окружность. Периметр трапеции равен 72, средняя линия равна 14. Найдите боковую сторону трапеции.
Вероятность того, что в случайный момент времени температура тела здорового человека окажется ниже чем 36,7°, равна 0,62. Найдите вероятность того, что в случайный момент времени у здорового человека температура окажется 36,7° или выше.
Найдите корень уравнения [math]\log_\frac17(5-x)=-2[/math]
В тупоугольном треугольнике KLM KL = LM = 18, КН — высота, LH = 9. Найдите cos ∠KLM.
Прямая у = 24х + 5 является касательной к графику функции у = 32х2 + bх + 7. Найдите значение b, учитывая, что абсцисса точки касания больше 0.
Сосуд в виде правильной треугольной пирамиды высотой 25√3 см до верха заполнен водой. Найдите, на какой высоте будет находиться уровень воды, если её перелить в другой сосуд, имеющий форму куба со стороной, равной стороне основания данной треугольной пирамиды. Ответ выразите в сантиметрах.
Найдите 45а - 19b + 40, если [math]\frac{3a-5b+7}{8a-4b+7}=6[/math].
Амплитуда колебаний маятника зависит от частоты вынуждающей силы и определяется по формуле [math]A\left(\omega\right)=\frac{A_0\omega_p^2}{\vert\omega_p^2-\omega^2\vert}[/math], где [math]\omega[/math] — частота вынуждающей силы (в с-1), А0 — постоянный параметр, [math]\omega_p[/math] = 350 c-1 — резонансная частота. Найдите максимальную частоту [math]\omega[/math] (в с-1), меньшую резонансной, для которой амплитуда колебаний превосходит величину А0 не более чем на [math]\frac{A_0}{24}[/math]. Ответ выразите в с-1.
Два гонщика участвуют в гонках. Им предстоит проехать 15 кругов по кольцевой трассе с протяженностью круга 9,6 км. Оба гонщика стартовали одновременно, а на финиш первый пришел раньше второго на 12 мин. Чему равнялась скорость второго гонщика, если известно, что первый гонщик в первый раз обогнал второго на круг через 1 час 12 мин? Ответ дайте в км/ч.
Найдите точку максимума функции у = (х — 6)2(х + 9) + 3.
Часть 2.
При выполнении заданий 13—19 требуется записать полное решение и ответ.
а) Решите уравнение [math]\sin3x=2\cos\left(\frac{\mathrm\pi}2-x\right)[/math].
б) Найдите все корни этого уравнения, принадлежащие промежутку (-3π/2; 0].
Решение:
[math]\sin3x=3\sin x-4\sin^3x[/math]
[math]\begin{array}{l}3\sin x-4\sin^3x=2\sin x\\4\sin^3x-\sin x=0\\\sin x(4\sin^2x-1)=0\\\sin x=0;\;x=\mathrm{πn},\;\mathrm n\in\mathbb{Z}\\\mathrm{sinx}=\pm\frac12;\;\mathrm x=\pm\frac{\mathrm\pi}6+\mathrm{πk},\;\mathrm k\in\mathbb{Z}\end{array}[/math]
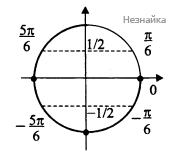
С помощью числовой окружности отберем корни, принадлежащие указанному промежутку:
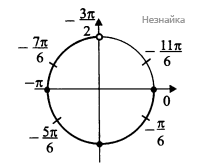
Ответ: а) [math]\mathrm{πn},\;\mathrm n\in\mathbb{Z};[/math]
[math]\pm\frac{\mathrm\pi}6+\mathrm{πk},\;\mathrm k\in\mathbb{Z};[/math]
б) [math]-\frac{7\mathrm\pi}6,\;-\mathrm\pi,\;-\frac{5\mathrm\pi}6,\;-\frac{\mathrm\pi}6,\;0[/math]
Около шара описана правильная усечённая четырёхугольная пирамида, у которой площадь одного основания в 9 раз больше площади другого.
а) Докажите, что боковыми гранями усечённой пирамиды являются трапеции, высоты которых равны среднему арифметическому сторон оснований.
б) Найдите угол наклона боковой грани к плоскости основания.
Решение:
а) Рассмотрим усеченную четырехугольную пирамиду [math]ABCDA_1B_1C_1D_1[/math], Описанную около шара (см. рисунок) Пусть [math]A_1B_1C_1D_1[/math] - квадрат со стороной а, [math]ABCD[/math] - квадрат со стороной b. По условию [math]S_{ABCD}=9S_{A_1B_1C_1D_1}[/math] , [math]b^2=9a^2[/math] следовательно [math]b=3a[/math].
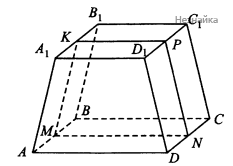
Пусть [math]M[/math] - середина [math]AB[/math], [math]N[/math] - середина [math]CD[/math]. Проведем прямую [math]MN[/math] сечение, перпендикулярное плоскости основания. Пусть [math]KP[/math] - отрезок, по которому плоскость сечения пересекается с верхним основанием, [math]KP\parallel MN[/math], [math]K[/math] - середина [math]A_1B_1[/math], [math]P[/math] - середина [math]C_1D_1[/math]. Трапеция [math]KPMN[/math] описана около круга, образованного сечением шара рассматриваемой плоскостью. Тогда [math]KP+MN=MK+PN=4a[/math], [math]MK=PN=2a[/math]. C другой стороны, [math]PN[/math] - высота трапеции [math]DD_1C_1C[/math] и [math]PN=2a=\frac{3a+a}2=\frac{CD+C_1D_1}2[/math], что и требовалось доказать.
б) Рассмотрим трапецию [math]MKPN[/math] (см. рисунок)
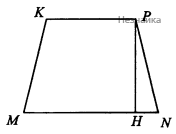
[math]MN\perp CD[/math], [math]PN\perp CD[/math], поэтому [math]\angle PNM[/math] - линейный угол искомого двугранного угла
[math]HN=\frac{MN-KP}2=\frac{3a-a}2=a[/math]
[math]\cos\angle PNH=\frac{HN}{PN}=\frac a{2a}=\frac12[/math]
[math]\angle PNH=\frac{\mathrm\pi}3[/math]
Ответ: [math]\frac{\mathrm\pi}3[/math]
Решите систему неравенств [math]\left\{\begin{array}{l}4^x-2^{2(x-1)}+8^{\frac23(x-2)}>52,\\2\log_\frac12(x-2)-\log_\frac12(x^2-x-2)\geq1.\end{array}\right.[/math]
Решение:
1)[math]4^x-2^{2(x-1)}+8^{\frac23(x-2)}>52[/math]
[math]2^{2(x-1)}=4^{x-1}=\frac{4^x}4;[/math][math]8^{\frac23(x-2)}=4^{x-2}=\frac{4^x}{16};[/math]
[math]4^x-\frac{4^x}4+\frac{4^x}{16}>52,\frac{13}{16}4^x>52,\;x>3,\;x\in\left(3;+\infty\right)[/math]
2) ОДЗ: [math]\begin{array}{l}\left\{\begin{array}{l}x-2>0\\x^2-x-2>0\end{array}\right.x>2\\\end{array}[/math]
[math]\begin{array}{l}\log_\frac12\frac{(x-2)^2}{(x+1)(x-2)}\geq1\\\end{array}[/math], [math]\begin{array}{l}\frac{(x-2)^2}{(x+1)(x-2)}\leq\frac12\\\end{array}[/math], [math]\begin{array}{l}\frac{(x-2)}{(x+1)}\leq\frac12\\\end{array}[/math], [math]\begin{array}{l}\frac{(x-5)}{2(x+1)}\leq0\\\end{array}[/math].
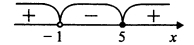
[math]\begin{array}{l}x\in(-1;5\;\rbrack\\\end{array}[/math], с учетом ОДЗ [math]\begin{array}{l}x\in(2;5\;\rbrack\\\end{array}[/math]
3) [math]\begin{array}{l}(2;5\;\rbrack\cap(3,+\infty)=\;(3;5\rbrack.\\\end{array}[/math]
Ответ: [math]\begin{array}{l}x\in(3;5\rbrack.\\\end{array}[/math]
В выпуклом четырёхугольнике ABCD на сторонах AD и CD взяты точки М и N, такие, что каждая из прямых СМ и AN делит ABCD на две фигуры равных площадей.
а) Докажите, что АС параллельно MN.
б) Найдите отношение площадей четырёхугольников ABCD и АВСО, где О — точка пересечения BD и MN.
Решение:
Из условия следует, что [math]S_{AND}=S_{MCD}=\frac12S_{ABCD}[/math] (см. рисунок)
Но тогда для треугольников [math]AND[/math] и [math]MCD[/math] с общим углом [math]D[/math] имеем [math]\frac12AD\times ND\times\sin\angle D=\frac12MD\times CD\times\sin\angle D[/math] или [math]\frac{AD}{MD}=\frac{CD}{ND}[/math] . Следовательно, треугольники [math]MND[/math] и [math]ACD[/math] подобны по второму признаку подобия, из чего следует, что [math]AC\parallel MN[/math].
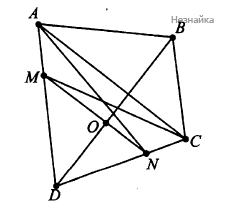
б) Так как [math]AC\parallel MN[/math], то точки [math]O[/math] и [math]N[/math] равноудалены от прямой [math]AC[/math], а значит, высоты треугольников [math]AOC[/math] и [math]ANC[/math] равны, поэтому их площади также равны. Следовательно, [math]S_{ANCB}=S_{ABC}+S_{AOC}=S_{ABCO}[/math], но [math]S_{ANCB}[/math] по площади составляет половину от [math]S_{ABCD}[/math], поэтому и [math]S_{ABCO}[/math] составляет половину от [math]S_{ABCD}[/math] по площади.
Ответ: 2:1
Незнайка несколько лет назад вложил деньги в акции некоторого предприятия. Ежегодно он получал прибыль по акциям сначала 9 1/11% в год, потом 37,5% в год и наконец 6 2/3% в год и сразу же вкладывал деньги в те же акции. Известно, что одинаковые процентные ставки были равное число лет, а в конце первоначальная сумма его вклада увеличилась на 156%. Определите срок хранения вклада.
Решение:
Увеличение вклада на [math]9\frac1{11}\%[/math] увеличивает его в [math](100+9\frac1{11})\div100[/math] раз, или в [math]\frac{12}{11}[/math] раза. Аналогично увеличение на [math]37,5\%[/math] увеличивает вклад в [math]\frac{550}{400}[/math] раза, увеличение на [math]6\frac23\%[/math] - в [math]\frac{16}{15}[/math] раза. Если каждая процентная ставка была [math]k[/math] лет, то вклад увеличился в [math]\left(\frac{12}{11}\times\frac{55}{40}\times\frac{16}{15}\right)^k[/math] раз, что по условию равно [math]\frac{100+156}{100}[/math] или [math]\frac{64}{25}[/math] раза.
[math]\left(\frac{12}{11}\times\frac{55}{40}\times\frac{16}{15}\right)^k=\frac{64}{25},\;\left(\frac85\right)^k=\frac{64}{25};\;k=2[/math]
Всего вклад хранился [math]3\times2=6\;лет[/math]
Ответ: 6 лет.
При каких значениях р > 0 уравнение [math]3\sqrt{2x+p}=1+3x[/math] имеет два различных корня?
Решение:
Обозначим [math]y=\sqrt{2x+p}\geq0,\;[/math] тогда [math]x=\frac{y^2-p}2[/math] и уравнение примет вид [math]3y^2-6y+2=3p[/math]
Построим графики [math]z=3y^2-6y+2,\;y\geq0[/math] и [math]z=3p[/math] (см. рисунок)
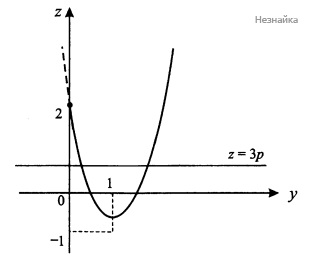
Находим абсциссу вершины параболы: [math]y_0=\frac6{2\times3}=1[/math]; Ордината вершины параболы [math]z_0=z(1)=-1[/math]. Очевидно, что искомые [math]p[/math] должны удовлетворять условию [math]-1<3p\leq2[/math], отсюда [math]-\frac13<p\leq\frac23[/math], А с учетом условия задачи [math]0<p\leq\frac23[/math]
Ответ: [math]0<p\leq\frac23[/math]
Решите в целых числах уравнение 19х2 + 28у2 = 729.
Решение:
Так как [math](18x^2+27y^2)+(x^2+y^2)=729[/math], то [math]x^2+y^2[/math] делится на 3, поэтому [math]x:3[/math] и [math]y:3[/math].
Действительно, пусть [math]x^2+y^2=3m\;(m\in\mathbb{N})[/math]. Предположим, что [math]x[/math] не делится на 3. Тогда либо [math]x=3t+1[/math], либо [math]x=3t+2\;(t\in\mathbb{Z})[/math]. В любом случае [math]x^2=3k+1\;(k\in\mathbb{Z})[/math]. Отсюда получаем: [math]3m=x^2+y^2=3k+1+y^2[/math]
Поэтому [math]1+y^2[/math] делится на 3. Но согласно вышесказанному, [math]y^2=3s+1(s\in\mathbb{Z})[/math]. Получаем, что [math]3m=3(k+s)+2[/math], что невозможно.
Пусть [math]x=3u,\;y=3v\;(u,v\in\mathbb{Z})[/math], тогда [math]19u^2+28v^2=81[/math]. Повторяя рассуждения, получим, что [math]u=3a,\;v=3b\;(a,b\in\mathbb{Z})[/math] и [math]19a^2+28b^2=9[/math]. Это уравнение не имеет решения в целых числах, так как [math]19a^2+28b^2[/math] либо равно нулю, либо не меньше [math]19[/math].
Ответ: решений нет
| № | Ваш ответ | Ответ и решение | Первичный балл |
|---|---|---|---|
|
Здесь появится результат первой части. Нажмите на кнопку «Завершить работу», чтобы увидеть правильные ответы и посмотреть решения. |
|||