Вариант 13
Математика Профильный уровень
Часть 1
Ответом на задания 1—12 должно быть целое число или десятичная дробь.
Клиент взял в кредит 25 000 рублей на полгода под 20%. Он должен погашать кредит, внося в банк ежемесячно одинаковую сумму денег, с тем чтобы через полгода выплатить всю сумму, взятую в кредит, вместе с процентами. Сколько рублей он должен вносить в банк ежемесячно?
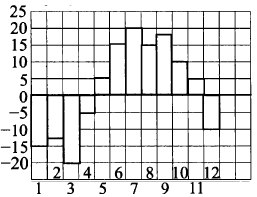
На диаграмме 70 показана среднемесячная температура воздуха в городе Новолесенск за каждый месяц 1964 года. По горизонтали указываются месяца, по вертикали — температура в градусах Цельсия. Определите по диаграмме наибольшую среднемесячную температуру во второй половине 1964 года. Ответ дайте в градусах Цельсия.
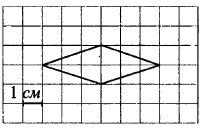
Найдите площадь ромба, изображённого на клетчатой бумаге с размером клетки 1 см х 1 см. Ответ дайте в квадратных сантиметрах.
У Максима есть денежные монеты достоинством 1 рубль — 12 штук, 2 рубля — 5 штук, 5 рублей — 3 штуки, 10 рублей — 4 штуки. Наугад он достаёт одну монету и подбрасывает её. Какова вероятность того, что выпадет орёл пятирублёвой монеты?
Найдите корни уравнения [math]tg\frac{\mathrm\pi\left(2\mathrm x+1\right)}4=-1[/math], в ответе запишите наибольший отрицательный корень.
В треугольнике АВС угол С равен 90°, высота СН равна 6, ВН = 12√6. Найдите cos А.
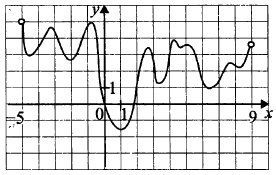
На рисунке изображён график функции у = F(x) — одной из первообразной некоторой функции f(x), определённой на интервале (-5; 9). Пользуясь рисунком, определите количество решений уравнения f(x) = 0 на отрезке [-3; 6].
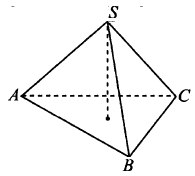
Найдите высоту правильной треугольной пирамиды, стороны основания которой равны 6 и объём равен 12√3.
Найдите значение выражения [math]y=2x+\sqrt{4x^2-24x+36}[/math] при [math]x=3[/math].
Деталью некоторого прибора является вращающаяся катушка. ( состоит из трёх однородных соосных цилиндров: центрального массой m = 5 кг и радиуса R = 8 см и двух боковых с массами М = 2 кг и радиусами R + h, где h - добавочная высота цилиндра. При этом момент инерции катушки относительно вращения, выражаемый в кг • см2, задаётся формулой [math]I=\frac{\left(m+2M\right)R^2}2+M\left(2Rh+h^2\right)[/math]. При каком максимальном значении добавочной высоты h момент инерции катушки не превышает предельного значения 402 кг • с. Ответ выразите в сантиметрах.
Смешали 5 л 27%-ного водного раствора некоторого вещества с 8 л 40%-ного водного раствора этого же вещества. Сколько процентов составляет концентрация-получившегося раствора?
Найдите наибольшее значение функции у = (х2 + 5х - 5)е7-х на отрезке [7; 15].
Часть 2.
При выполнении заданий 13—19 требуется записать полное решение и ответ.
а) Решите уравнение [math]\sin\left(3\pi-2x\right)+1=\cos\left(\frac\pi2-x\right)-\cos\left(\pi-x\right)[/math].
б) Найдите все корни этого уравнения, принадлежащие промежутку [π/2 ; 2π).
Решение:
[math]\sin2x+1=\sin x+\cos x;[/math] [math]2s\mathrm{in}x\cos x+\cos^2x+\sin^2x=\sin x+\cos x;[/math][math](\sin x+\cos x)^2=\sin x+\cos x;[/math][math](\sin x+\cos x)(\sin x+\cos x-1)=0;[/math]
[math]\begin{array}{l}\left\{\begin{array}{l}\sin x+\cos x=0\\\sin x+\cos x=1\end{array}\right.\\\left\{\begin{array}{l}\frac{\sqrt2}2\sin x+\frac{\sqrt2}2\cos x=0\\\frac{\sqrt2}2\sin x+\frac{\sqrt2}2\cos x=\frac{\sqrt2}2\end{array}\right.\\\left\{\begin{array}{l}\sin(x+\frac{\mathrm\pi}4)=0\\\sin(x+\frac{\mathrm\pi}4)=\frac{\sqrt2}2\end{array}\right.\\\left\{\begin{array}{l}x=-\frac{\mathrm\pi}4+\mathrm{πn},\;\mathrm n\in\mathbb{Z}\\x=-\frac{\mathrm\pi}4+(-1)^k\frac{\mathrm\pi}4+\mathrm{πk},\;\mathrm n\in\mathbb{Z}\end{array}\right.\\\end{array}[/math]
б) Найдем все корни уравнения, принадлежащие промежутку [math]\lbrack\frac{\mathrm\pi}2;2\mathrm\pi)[/math]
[math]\begin{array}{l}n=1,\;x=\frac{3\mathrm\pi}4\\n=2,\;x=\frac{7\mathrm\pi}4\\k=1,\;x=\frac{\mathrm\pi}2\end{array}[/math]
Ответ: а) [math]-\frac\pi4+\pi\kappa,\;-\frac{\mathrm\pi}4+(-1)^k\frac{\mathrm\pi}4+\mathrm{πk},\;\mathrm n\in\mathbb{Z};[/math]
б) [math]\frac\pi2;\;\frac34\pi;\;\frac74\pi[/math]
Дана правильная четырёхугольная пирамида, сторона основания которой равна 18, а высота равна 24.
а) Постройте сечение, проходящее через две противоположные вершины основания и перпендикулярное одному из боковых рёбер.
б) Найдите косинус угла между смежными боковыми гранями.
Решение:
а) Рассмотрим правильную четырехугольную пирамиду [math]\mathrm{EABCD}[/math] и построим сечение, проходящее через вершины [math]\mathrm B[/math] и [math]\mathrm D[/math], перпендикулярное ребру [math]\mathrm{AE}[/math]. Проведем [math]\mathrm{BK}\perp\mathrm{AE}[/math] и докажем, что [math]DK\perp AE[/math] (см. рисунок (а) )
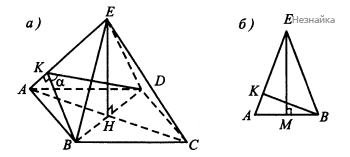
В треугольниках [math]AKB[/math] и [math]AKD[/math] сторона [math]AK[/math] - общая, [math]AB=AD[/math] и [math]\angle BAK=\angle DAK[/math]. Следовательно [math]\bigtriangleup AKB=\bigtriangleup AKD[/math] по первому признаку равенства треугольников. Поэтому [math]\angle AKB=\angle AKD=90^\circ[/math]. Значит, [math]AE\perp DK[/math] и [math]AE\perp[/math] плоскости [math]BKD[/math]. Таким образом, [math]BKD[/math] - искомое сечение.
б) Пусть [math]EH[/math] - высота пирамиды [math]EABCD[/math].
[math]AC=BD=AB\sqrt2=18\sqrt2[/math], [math]AH=\frac12AC=9\sqrt2[/math] [math]AE=\sqrt{AH^2+EH^2}=\sqrt{(9\sqrt2)^2+24^2}=\sqrt{738}[/math]
Рассмотрим равнобедренный треугольник [math]ABE[/math] (см. рисунок (б)). Апофему [math]EM[/math] найдем из [math]\bigtriangleup MBE[/math], учитывая, что [math]MB=\frac12AB=9[/math].
[math]EM=\sqrt{BE^2-MB^2}=\sqrt{738-81}=\sqrt{657}[/math]
найдем высоту [math]BK[/math] из формулы площади [math]\bigtriangleup AEB[/math].
[math]S_{AEB}=\frac12EM\times AB=\frac12EA\times BK[/math]
Отсюда [math]BK=\frac{EM\times AB}{EA}=18\frac{\sqrt{657}}{\sqrt{738}}[/math]
Так как [math]\bigtriangleup AKB=\bigtriangleup AKD[/math], то [math]DK=BK[/math]. По теореме косинусов для [math]\bigtriangleup BKD:[/math] [math]BD^2=DK^2+BK^2-2DK\times BK\times\cos\alpha[/math], где [math]\alpha=\angle BKD[/math] - угол между смежными боковыми гранями.
[math]\begin{array}{l}\left(18\sqrt2\right)^2=\frac{657\times18^2}{738}\times2\times(1-\cos\alpha)\\\cos\alpha=-\frac9{73}\end{array}[/math]
Ответ: [math]-\frac9{73}[/math]
Решите систему неравенств [math]\left\{\begin{array}{l}\left(4\times4^x-5\times2^x+1\right)\times\log_{x+2,5}\vert x+0,5\vert\geq0,\\4^{x+1}+\log_{x+2,5}\vert x+0,5\vert+1\leq5\times2^x.\end{array}\right.[/math]
Решение:
Для удобства обозначим [math]4\times4^x-5\times2^x+1=a, log_{x+2,5}\left|x+0,5\right|=b [/math], тогда система неравенств примет вид: [math]\left\{\begin{array}{l}a\times b\geq0\\a+b\leq0\end{array}\right.[/math]. Полученная система с переменными [math]a[/math] и [math]b[/math] равносильна системе [math]\left\{\begin{array}{l}a\leq0\\b\leq0\end{array}\right.[/math]. Значит, данная система неравенств равносильна системе [math]\left\{\begin{array}{l}4\times4^x-5\times2^x+1\leq0\\\log_{x+2,5}\left|x+0,5\right|\leq0\end{array}\right.[/math]
Решим первое неравенство. Пусть [math]2^x=t[/math], тогда получим квадратное неравенство [math]4t^2-5t+1\leq0[/math], имеющее решения [math]\frac14\leq t\leq1[/math]. Отсюда из двойного неравенства [math]\frac14\leq2^x\leq1[/math] имеем [math]-2\leq x\leq0[/math]
2) Найдем область определения второго неравенства последней системы:
[math]\left\{\begin{array}{l}\begin{array}{c}x+2,5>0\\x+2,5\neq1\end{array}\\\left|x+0,5\right|>0\end{array}\right.\;\left\{\begin{array}{l}\begin{array}{c}x>-2,5\\x\neq-1,5\end{array}\\x\neq-0,5\end{array}\right.\left\{\begin{array}{l}-2,5<x<-1,5\\\begin{array}{c}-1,5<x<-0,5\;и\;x>-0,5\end{array}\end{array}\right.[/math]
используя рационализацию второго неравенства на области его определения, получаем:
[math]\begin{array}{l}(x+2,5-1)(\left|x+0,5\right|-1)\leq0;\\(x+1,5)(\left(x+0,5\right)^2-1)\leq0;\\(x+1,5)(x+1,5)(x-0,5)\leq0;\\(x+1,5)^2(x-0,5)\leq0;\end{array}[/math]
Для решения последнего неравенства применяем метод интервалов. Получаем, что [math]x\in(-\infty;0,5\rbrack[/math]
Учитывая ОДЗ переменной второго неравенства системы, получаем значения:
[math]x\in(-2,5;\;-1,5)\cup(-1,5;\;-0,5)\cup(-0,5;0,5\rbrack[/math]
3) Найдем общую часть полученных решений неравенств системы:
[math]x\in\lbrack-2;\;-1,5)\cup(-1,5;\;-0,5)\cup(-0,5;0\rbrack[/math]
Ответ: [math]x\in\lbrack-2;\;-1,5)\cup(-1,5;\;-0,5)\cup(-0,5;0\rbrack[/math]
Радиусы двух окружностей с центрами О1 и О2, касающихся внутренним образом в точке А, равны 5 и 4 соответственно. Их общая секущая, проведённая через точку А, пересекает первую окружность в точке В, вторую — в точке С.
а) Докажите, что [math]\frac{AB}{AO_1}=\frac{BC}{O_1O_2}[/math].
б) Найдите длину касательной, проведённой из точки В ко второй окружности, если дополнительно известно, что АВ = 1.
Решение:
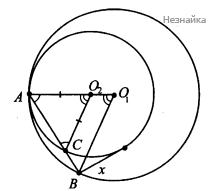
а) Рассмотрим случай, когда прямые [math]BC[/math] и [math]O_1O_2[/math] не совпадают. Тогда [math]\bigtriangleup O_2AC[/math] и [math]\bigtriangleup O_1AB[/math] - равнобедренные и, следовательно, [math]\angle O_2AC=\angle O_2CA,\;[/math][math]\angle O_1AC=\angle O_1BC\;[/math], но [math]\angle O_2AC[/math] - общий, поэтому [math]\angle O_2AC=\angle O_1AC=\angle O_1BC=\angle O_2CA[/math] и [math]\bigtriangleup O_2AC\;\sim\;\bigtriangleup O_1AB[/math] по двум углам и [math]\frac{AC}{AB}=\frac{AO_2}{AO_1}[/math]
[math]\begin{array}{l}\frac{BC}{AB}=\frac{AB-AC}{AB}=1-\frac{AC}{AB}\\\frac{O_1O_2}{AO_1}=\frac{AO_1-AO_2}{AO_1}=1-\frac{AO_2}{AO_1}\end{array}[/math]
Значит, [math]\frac{BC}{AB}=\frac{O_1O_2}{AO_1}[/math] или [math]\frac{BC}{O_1O_2}=\frac{AB}{AO_1}[/math] (см. рисунок)
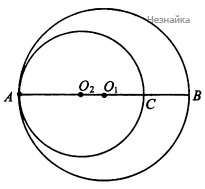
Рассмотрим случай, когда прямые [math]O_1O_2[/math] и [math]AB[/math] совпадают:
[math]\frac{AB}{AO_1}=2;[/math][math]BC=AB-AC=10-8=2[/math]; [math]O_1O_2=AO_1-AO_2=1[/math]; [math]\frac{BC}{O_1O_2}=2=\frac{AB}{AO_1}[/math] (см. рисунок)
б) Обозначим [math]x[/math] - искомая длина касательной, тогда [math]\begin{array}{l}x^2=AB\times BC=AB^2\times\frac{O_1O_2}{AO_1}=\frac15\\x=\frac{\sqrt5}5\end{array}[/math]
Ответ: [math]x=\frac{\sqrt5}5[/math]
В течение года цена дивана два раза увеличивалась на один и тот же процент. Первоначальная цена составляла 10000 рублей. После второго повышения она составила 12 100 рублей. На сколько процентов повысилась цена оба раза?
Решение:
Пусть на [math]x\%[/math] повышалась цена дивана ежегодно, тогда [math]10000\left(1+\frac x{100}\right)^2[/math] рублей цена дивана после второго повышения. По условию новая цена дивана составила 12100 рублей. Составим и решим уравнение
[math]10000\left(1+\frac x{100}\right)^2=12100,\;x>0[/math]
x=10
Цена дивана повысилась на 10%
Ответ: 10
При каких значениях параметра а система [math]\left\{\begin{array}{l}y=x^2+2x-5,\\y=3a-2x\end{array}\right.[/math] имеет ровно одно решение на отрезке х ∈ [-3;2]?
Решение:
Схематически изобразим график функции [math]y_1=x^2+2x-5[/math] при [math]x\in\lbrack-3;2\rbrack[/math]. Это фрагмент параболы с вершиной (-1;-6). При этом [math]y_2=3a-2x[/math] - это семейство параллельных прямых. Очевидно, что искомые значения параметра принадлежат [math](a_1;a_2\rbrack\cup\left\{a_3\right\}[/math], если точка касания, соответствующая [math]a_3[/math], принадлежит отрезку [math]\lbrack-3;2\rbrack[/math] и [math]a\in(a_1;a_2\rbrack[/math] в противном случае. Учитывая, что [math]y_1(-3)=-2;\;y_1(2)=3,\;[/math] определим координаты точек [math]A[/math] и [math]B[/math]: [math]A(-3;-2),\;B(2;3)[/math]
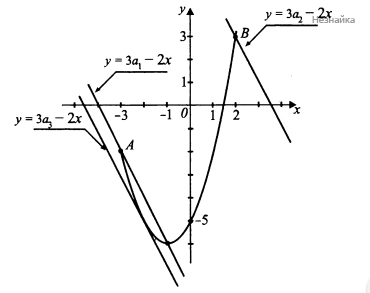
[math]a_1:\;-2=3a-2(-3);\;a=-\frac83[/math]
[math]a_2:\;3=3a-2\times2;\;a=\frac73[/math]
Определим [math]a_3[/math]: уравнение [math]x^2+2x-5=3a-2x[/math] должно иметь единственное решение. Это будет в случае, когда дискриминант равен нулю. [math]D=36+12a=0;\;a=-3[/math]. В этом случае решением уравнения будет [math]x=-2\;\in\left[-3;2\right][/math]
Ответ: {-3}⋃(-8/3; 7/3]
На доске выписана последовательность a1, a2, ... a1010, при этом а1 = 3.
В каждом из следующих случаев определите а1000
а) Для любого натурального к среднее арифметическое первых к членов последовательности равно 3.
б) Для любого натурального к ≥ 2 среднее арифметическое первых к членов последовательности на 1 больше среднего арифметического первых (к — 1) членов последовательности.
в) Для всех нечётных натуральных к среднее арифметические первых k членов последовательности равны между собой и на 1 меньше средних арифметических первых 2m членов последовательность для любого натурального m.
Решение: а) Покажем, что все [math]a_k=3.[/math] Действительно: [math]\frac{a_1+a_2}2=3;[/math] [math]a_2=2\times3-a_1=3;[/math] [math]\frac{a_1+a_2+a_3}3=3[/math]; [math]a_3=3\times3-a_1-a_2=3;\;...[/math]
Если [math]a_1=a_2=...=a_n=3[/math] и [math]\frac{a_1+a_2+a_3+...+a_{n+1}}{n+1}=3[/math], то [math]a_{n+1}=3(n+1)-a_1-a_2-...-a_n=3(n+1)-3n=3[/math]. Значит, [math]a_{1000}=3[/math].
б) Пусть среднее арифметическое первых n чисел равно [math]x_n[/math]. Тогда сумма первых n чисел равна [math]nx_n[/math], откуда [math]x_{n+1}=\frac{nx+a_{n+1}}{n+1}.[/math] С другой стороны, по условию [math]x_{n+1}=x_n+1[/math], откуда [math]x_n+1=\frac{nx+a_{n+1}}{n+1}[/math] и [math]a_{n+1}=n+x_n+1[/math].
Учитывая, что [math]x_n[/math] образуют арифметическую прогрессию с разностью 1, получим [math]x_n=3+(n-1)=n+2[/math] и [math]a_{n+1}=2n+3=2(n+1)+1[/math], значит, [math]a_n=2n+1[/math] и [math]a_{1000}=2001; [/math]
в) Для любого нечетного [math]k[/math] среднее арифметическое первых [math]k[/math] чисел равно 3, так как при [math]k=1[/math] среднее арифметическое равно 3. Для четных [math]k[/math] среднее арифметическое равно 4. Тогда для четных [math]k[/math] [math]\frac{3(k-1)+a_k}k=4[/math]. [math]a_k=k+3;\;a_{1000}=1003[/math]
Ответ: а) 3 б) 2001 в) 1003
| № | Ваш ответ | Ответ и решение | Первичный балл |
|---|---|---|---|
|
Здесь появится результат первой части. Нажмите на кнопку «Завершить работу», чтобы увидеть правильные ответы и посмотреть решения. |
|||