Вариант 10
Математика Профильный уровень
Часть 1
Ответом на задания 1—12 должно быть целое число или десятичная дробь.
Коля отправил SMS-сообщения своим 15 друзьям. Стоимость одного SMS-сообщения равна 1 рубль 20 копеек. Перед отправкой сообщения на счету у Коли было 50 рублей. Сколько рублей останется у Коли после отправки всех сообщений?
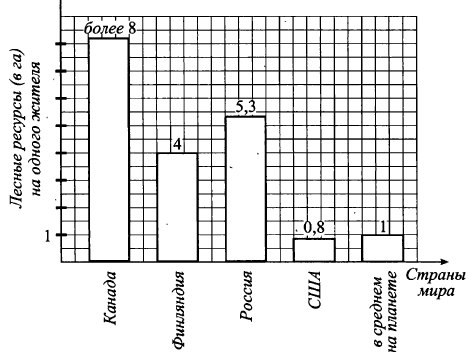
На диаграмме показано обеспечение каждого жителя планеты лесными ресурсами. По горизонтали отмечены страны мира, по вертикали — лесные ресурсы на каждого жителя в гектарах. Определите по диаграмме разность между средним обеспечением лесными ресурсами по планете и в США.
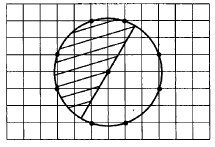
Найдите (в см2) площадь S закрашенной фигуры, изображённой на клетчатой бумаге с размером клетки 1 см х 1 см. В ответе укажите S / π.
В папке у Димы Гущина лежат четыре пронумерованных цифрами 1, 2, 3, 4 файла с документами, а также заявление на отпуск. Доставая заявление на отпуск, Дмитрий Дмитриевич случайно вытащил и файл с документами. Найдите вероятность того, что он достал файл 3.
Решите уравнение [math]\frac{28}{x^2-36}=1[/math]. Если уравнение имеет более одного корня, в ответе укажите меньший из них.
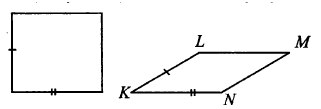
Параллелограмм и прямоугольник имеют одинаковые стороны. Найдите тупой угол параллелограмма, если его площадь равна половине площади прямоугольника. Ответ дайте в градусах.
Материальная точка движется прямолинейно по закону [math]x(t)=\frac{t^3}3-\frac{5t^2}2-6t+7[/math], где х — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. В какой момент времени (в секундах) её скорость была равна 8 м/c?
Длина окружности основания цилиндра равна 2. Площадь боковой поверхности равна 14. Найдите высоту цилиндра.
Найдите значение выражения [math]\frac{26}{\sin\left(-{\displaystyle\frac{47\pi}6}\right)\cdot\cos{\displaystyle\frac{32\pi}3}}[/math].
В баке, имеющем форму цилиндра, на боковой стенке у дна закреплён кран. После его открытия вода, находящаяся в баке, начинает вытекать, и высота столба воды (м) меняется по закону [math]H(t)=H_0-\sqrt{2gH_0}kt+\frac g2k^2t^2[/math]где t — время в секундах, прошедшее с момента открытия крана, Но = 20 м — начальная высота столба воды, k = 1/80 — отношение площадей поперечных сечений крана и бака, g — ускорение свободного падения (g = 10 м/сек2). Найдите, через сколько секунд после открытия крана в баке не станет воды.
Первый и второй насосы наполняют бассейн за 8 минут, второй и третий — за [math]\frac{16}3[/math] минут, первый и третий также за [math]\frac{16}3[/math] минут. За сколько минут эти три насоса заполнят бассейн, работая вместе?
Найдите наибольшее значение функции [math]y=\ln(x+7)^{11}-11x[/math] на отрезке [math]\left[-6,5;-4\right][/math].
Часть 2.
При выполнении заданий 13—19 требуется записать полное решение и ответ.
а) Решите уравнение [math]6\cos^2(x-\frac{3\mathrm\pi}2)-3\sqrt2\sin\;x=0[/math]
б) Укажите корни этого уравнения, принадлежащие отрезку [math]\left[-\frac{5\mathrm\pi}2;-\mathrm\pi\right][/math]
Решение:
а)[math]6\sin^2x-3\sqrt2\sin x=0[/math]
[math]6\sin x(\sin x-\frac{\sqrt2}2)=0[/math]
[math]\sin x=0[/math] или [math]\sin x=\frac{\sqrt2}2[/math]
[math]x=\mathrm{πn},\;\mathrm n\in\mathbb{Z}[/math]; [math]x=(-1)^k\frac{\mathrm\pi}4+k\mathrm\pi,\;\mathrm k\in\mathbb{Z}[/math]
б) [math]x\in\left[\frac{-5\mathrm\pi}2;-\mathrm\pi\right][/math]
[math]\begin{array}{l}n=1;\;x=-\mathrm\pi\\\mathrm n=-2;\;\mathrm x=-2\mathrm\pi\\\mathrm k=-1;\;\mathrm x=-\frac{5\mathrm\pi}4\\\mathrm k=-2;\;\mathrm x=-\frac{7\mathrm\pi}4\end{array}[/math]
Ответ: а)[math]x=(-1)^k\frac{\mathrm\pi}4+k\mathrm\pi,\;\mathrm k\in\mathbb{Z}[/math], [math]x=\mathrm{πn},\;\mathrm n\in\mathbb{Z}[/math]
б)[math]-\mathrm\pi;-2\mathrm\pi;-\frac{5\mathrm\pi}4;-\frac{7\mathrm\pi}4.[/math]
В основание цилиндра высотой 24 и радиусом основания 8 вписан тупоугольный треугольник АВС, в котором ВС = 12, АВ = АС.
а) Постройте сечение призмы ABCA1B1C1 плоскостью, перпендикулярной плоскостям BB1C1C и А1ВС и проходящей через точку А, если АА1, BB1 и CC1 — образующие цилиндра
б) Найдите величину угла между плоскостями (B1BC) и (A1BC).
Решение:
а) Пусть [math]O[/math] и [math]O_1[/math] - центры оснований цилиндра, тогда [math]F[/math] и [math]F_1[/math] - середины хорд [math]BC[/math] и [math]B_1C_1[/math] соответственно (см. рисунок). Покажем, что [math]AFF_1[/math] - искомая плоскость. [math]A_1F[/math] - медиана, а значит, и высота равнобедренного треугольника [math]A_1BC[/math]. [math]FF_{1\;}\parallel\;BB_1[/math], значит, [math]FF_{1\;}\perp\;(ABC)[/math] и, в частности, [math]FF_{1\;}\perp\;BC[/math]. Итак, [math]FF_{1\;}\perp\;BC[/math] и [math]A_1F\;\perp\;BC[/math], тогда [math](AFF_1)\perp BC[/math], откуда [math](AFF_1)\perp A_1BC[/math] и [math](AFF_1)\perp BB_1C_1C[/math]. Сечением призмы [math]ABCA_1B_1C_1[/math] плоскостью [math]AFF_1[/math] является прямоугольник [math]ADD_1A_1[/math]
б) Угол между плоскостями [math]B_1BC[/math] и [math]A_1BC[/math] - это угол [math]A_1FF_1:[/math]
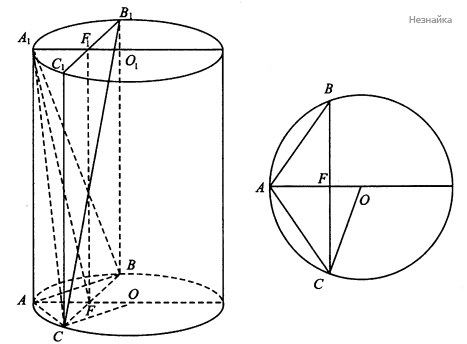
[math]A_1F\;\in\;(A_1BC)[/math], [math]FF_1\;\in\;(B_1BC)[/math]. [math]\bigtriangleup A_1CB\;[/math] - равнобедренный, [math]\;A_1F\perp BC,[/math] [math]B_1BCC_1[/math] - прямоугольник, [math]FF_1\;\parallel\;BB_1[/math] и [math]FF_1\;\perp\;BC[/math], отсюда [math]\angle A_1FF_1[/math] - линейный угол двугранного угла между плоскостями [math]A_1CB[/math] и [math]B_1BC[/math].
Из [math]\bigtriangleup A_1FF_1[/math]: [math]\angle A_1F_1F=90^\circ[/math] [math]tg\angle A_1FF_1=\frac{A_1F_1}{FF_1}[/math]; [math]A_1F_1=AF;\;AF=AO-FO.[/math]
Из [math]\bigtriangleup OFC[/math], где [math]\angle OFC=90^\circ[/math], [math]FC=6,[/math] найдем [math]FO=\sqrt{OC^2-FC^2}=2\sqrt7[/math]. [math]AF=8-2\sqrt7.[/math]
[math]tg\angle A_1FF_1=\frac{8-2\sqrt7}{24}=\frac{4-\sqrt7}{12}[/math]
[math]\angle A_1FF_1=arctg(\frac{4-\sqrt7}{12})[/math]
Ответ: [math]arctg(\frac{4-\sqrt7}{12})[/math]
Решите неравенство [math]\log_{0,5}\left(x-3\right)-\log_{0,5}\left(x+3\right)-\log_\frac{x+3}{x-3}2>0[/math].
Решение:
ОДЗ: [math]\left\{\begin{array}{l}\begin{array}{c}x-3>0\\x+3>0\\\frac{x+3}{x-3}>0\\\frac{x+3}{x-3}\neq1\end{array}\\x\neq3\end{array}\right.[/math]; x>3 или x<-3
[math]\log_{0,5}\left(\frac{x-3}{x+3}\right)-\frac1{\log_2\left(\frac{x+3}{x-3}\right)}>0[/math]
[math]-\log_2\left(\frac{x-3}{x+3}\right)+\frac1{\log_2\left(\frac{x-3}{x+3}\right)}>0[/math]
[math]\log_2\frac{x-3}{x+3}=t;\;-t+\frac1t>0[/math]
[math]\frac{t^2-1}t<0[/math]
[math]\log_2\frac{x-3}{x+3}<-1[/math] или [math]0<\log_2\frac{x-3}{x+3}<1[/math]
[math]\log_2\frac{x-3}{x+3}<\log_2\frac12[/math] или [math]\log_2\frac{x-3}{x+3}<\log_22[/math]
[math]\frac{x-3}{x+3}<\frac12[/math] или [math]1<\frac{x-3}{x+3}<2[/math]
Первое неравенство: [math]\frac{x-9}{2(x+3)}<0[/math]
[math]-3<x<9[/math]
Двойное неравенство: [math]\left\{\begin{array}{c}\frac{-6}{x+3}>0\\\frac{-x-9}{x+3}<0\end{array}\right.[/math]
[math]\left\{\begin{array}{c}x<-3\\x>-3\;или\;x<-9\end{array}\right.[/math]
Решение двойного неравенства: x<-9
Общее решение: или x<-9, или -3<x<9
Так как на ОДЗ x>3 или x<-3, получаем, что x<-9 или 3<x<9
Ответ: [math]x\in(-\infty;-9)\cup(3;9)[/math]
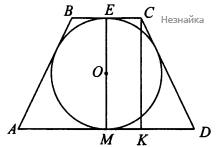
В равнобедренную трапецию вписана окружность.
а) Докажите, что диаметр окружности есть среднее пропорциональное между параллельными сторонами.
б) Найдите радиус этой окружности, если площадь трапеции равна 52, а параллельные стороны относятся как 3 : 5.
Решение:
а) Требуется доказать, что [math]EM^2=BC\times AD.[/math]
[math]ABCD[/math] - равнобедренная трапеция, [math]AB=DC[/math]
[math]CK\perp AD;\;CK=EM.[/math]
[math]\bigtriangleup CDK:\;\angle CDK=90^\circ,\;CK^2=CD^2-KD^2.[/math]
Учитывая, что четырехугольник [math]ABCD[/math] - описан, имеем [math]AB+CD=BC+AD,\;2AB=BC+AD,\;[/math][math]AB=\frac{BC+AD}2[/math]
[math]CK^2=\left(\frac{AD+BC}2\right)^2-\left(\frac{AD-BC}2\right)^2;[/math]
[math]CK^2=\left(\frac{AD+BC}2-\frac{AD-BC}2\right)\times\left(\frac{AD+BC}2+\frac{AD-BC}2\right)=BC\times AD.[/math]
[math]CK^2=BC\times AD,\;EM^2=BC\times AD.[/math] Что и требовалось доказать.
б) [math]\begin{array}{l}S_{TP}=\frac{AD+BC}2\times CK=\frac{AD+BC}2\times EM\\\end{array}[/math]
[math]\begin{array}{l}\frac{BC}{AD}=\frac35\\\end{array}[/math]. Пусть [math]\begin{array}{l}BC=3x\\\end{array}[/math], тогда [math]\begin{array}{l}AD=5x\\\end{array}[/math] [math]\begin{array}{l}BC+AD=8x\\\end{array}[/math],[math]\begin{array}{l}EM^2=3x\times15x=15x^2\\\end{array}[/math], [math]\begin{array}{l}EM=x\sqrt{15}\\\end{array}[/math]
Поставим в формулу площади трапеции:
[math]\begin{array}{l}52=\frac{8x\times x\sqrt{15}}2\\\end{array}[/math], [math]\begin{array}{l}x^2=\frac{13\sqrt{15}}{15}\\\end{array}[/math].
[math]\begin{array}{l}EM^2=15\times\frac{13\sqrt{15}}{15}=13\sqrt{15}\\\end{array}[/math]
[math]\begin{array}{l}EM=\sqrt{13\sqrt{15}}=2OM\\\end{array}[/math]
Ответ: [math]\begin{array}{l}OM=\frac{\sqrt{13\sqrt{15}}}2\\\end{array}[/math]
Гражданин Плюшкин выиграл по лотерейному билету в Британской национальной лотерее, в которой выигрыш не облагается налогом. На 800 тысяч долларов он купил предприятие, а остальные деньги положил в банк под 6% годовых от вложенной суммы.
В конце года выяснилось, что за год было реализовано продукции на 550 тысяч долларов, из них 350 тысяч долларов составили затраты производства (стоимость сырья, ремонт оборудования и т.п.) и 100 тысяч долларов уплачено персоналу. Остальные деньги составила прибыль гражданина Плюшкина. Через сколько лет общая сумма прибыли Плюшкина в первый раз превысит или будет равна начальному капиталу, вложенному в производство, если каждый год масштаб реализации продукции повышается на 10% от начального, затраты производства повышаются на 6% от первоначальных, а зарплата персонала увеличивается на 4% от первоначальной?
За первый год прибыль составила 550-350-100=100 тысяч долларов. Увеличение прибыли каждый год составляло [math]550\times0,1-350\times0,06-100\times0,04=30[/math] тысяч долларов. Запишем ряд чисел равных прибылям: 100,130,160,190,220,250....
Этот ряд представляет собой геометрическую прогрессию с первым членом 100 и разностью 30. Найдем номер наименьшего члена при котором сумма прогрессии будет не менее 800.
[math]S=\frac{2a_1+d(n-1)}2n[/math]
[math]\frac{200+30(n-1)}2n\geq800[/math]
[math]3n^2+17n-160\geq0[/math]
[math]3(n+\frac{32}3)(n-5)\geq0[/math]
[math]n\in(-\infty-\frac{32};3)(5;+\infty)[/math]
Ответ: 5 лет.
При каких значениях а уравнение [math]\left(\frac{2a+1}2\right)\sin3x+\cos^23x-1=\frac a2[/math] имеет ровно 3 корня, расположенных на отрезке [math]\left[\frac{4\mathrm\pi}3;\frac{5\mathrm\pi}3\right][/math]?
Решение:
[math]\frac{2a+1}2\sin3x-\frac a2-\sin^23x=0,[/math] пусть [math]\sin3x=t,\;\;-1\leq t\leq1[/math]
[math]t_1=\frac12,\;t_1=a.[/math]
1) [math]\sin3x=\frac12,[/math] 2) [math]\sin3x=a.[/math]
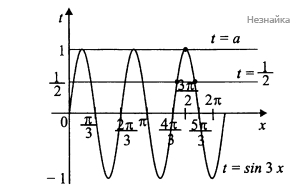
При [math]a=1[/math] данное уравнение имеет ровно три корня на отрезке [math]\left[\frac{4\mathrm\pi}3;\frac{5\mathrm\pi}3\right].[/math]
Ответ: а=1
Натуральные числа от 1 до n в порядке возрастания записаны в строчку. Под ними записаны те же числа в другом порядке. Можно ли добиться того, чтобы сумма каждого числа и записанного под ним была бы точным квадратом:
а) при n = 6;
б) при n = 13;
в) при n = 2014?
Решение:
а) Нельзя. С помощью первых шести натуральных чисел в сумме можно получить два точных квадрата 4 и 9. Под числом 1 может быть записано только число 3, но под числом 6 тоже может быть записано только число 3. Противоречие с условием задачи.
б) Можно. [math]\begin{array}{ccccccccccccc}1&2&3&4&5&6&7&8&9&10&11&12&13\\8&2&13&12&11&10&9&1&7&6&5&4&3\end{array}[/math]
в) Можно. Под каждым из чисел 102,103,.....,2013,2014 запишем числа 2014,2013,...,103,102 соответственно. тогда сумма чисел в каждом столбце, начиная со 102го, равна [math]2116=46^2[/math]. Под каждым из чисел 21,22,...,99,100,101 запишем числа 101,100,99,...,22,21. тогда сумма чисел с 21го по 101й равна [math]121=11^2[/math]. Под каждым из чисел 16,17,18,19,20 запишем числа 20,19,18,17,16. Тогда сума чисел в каждом столбце, с 16го по 20, равна [math]36=6^2[/math]. Под каждым из чисел 1,2,...,14,15 запишем числа 15,14,...,2,1. Тогда сумма чисел в каждом столбце,с 1го по 15й, равна [math]16=4^2[/math]
а) нельзя б) можно в) можно| № | Ваш ответ | Ответ и решение | Первичный балл |
|---|---|---|---|
|
Здесь появится результат первой части. Нажмите на кнопку «Завершить работу», чтобы увидеть правильные ответы и посмотреть решения. |
|||