Вариант 8
Математика Профильный уровень
Часть 1
Ответом на задания 1—12 должно быть целое число или десятичная дробь.
В пачке 500 листов бумаги формата А4. За неделю расходуется 3350 листов. Какое наименьшее количество пачек бумаги нужно купить в офис на одну неделю?
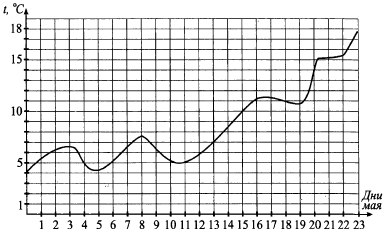
На рисунке показано изменение температуры воздуха с 1 по 23 мая. По горизонтали отмечены числа месяца, по вертикали — значение температуры в градусах Цельсия. Определите по рисунку, какого числа в период с 3 по 12 мая температура достигла наибольшего значения.
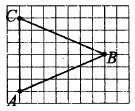
Найдите биссектрису треугольника АВС, проведённую из вершины В, если стороны квадратных клеток равны 1 см
Вероятность того, что электронная книга прослужит больше трёх лет, равна 0,86. Вероятность того, что она прослужит больше пяти лет, равна 0,72. Найдите вероятность того, что она прослужит меньше пяти лет, но больше трёх.
Найдите корень уравнения [math]\sqrt{3x^2+6x+1}=7-x[/math] если уравнение имеет более одного корня, то в ответе запишите больший.
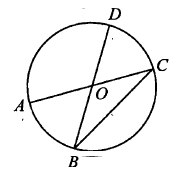
АС и BD — диаметры окружности с центром О. Угол АСВ равен 27°. Найдите угол AOD. Ответ дайте в градусах.
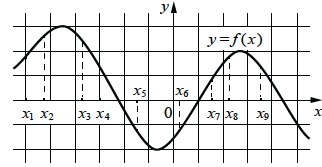
На рисунке изображён график дифференцируемой функции y = f(x). На оси абсцисс отмечены девять точек: x1 , x2 , ..., x9. Среди этих точек найдите все точки, в которых производная функции f (x) отрицательна. В ответе укажите количество найденных точек.
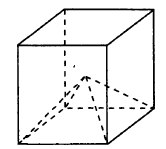
Объём куба равен 60. Найдите объём четырёхугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.
Найдите значение выражения [math]16\cos(\mathrm\pi+\mathrm\beta)\times\sin(\frac{7\mathrm\pi}2+\mathrm\beta)[/math], если [math]\mathrm{cosβ}=\frac12[/math]
Камнеметательная машина выстреливает камни под некоторым острым углом к горизонту. Траектория полёта камня описывается формулой [math]y=ax^2+bx+c,\;[/math] где [math]a=-\frac1{450}м^{-1},\;b=\frac13,\;c=1м[/math] — постоянные параметры, х — смещение камня по горизонтали, у — высота камня над землёй. Найдите, на каком наибольшем расстоянии в метрах от крепостной стены высотой 12,5 м нужно установить камнеметательную машину, чтобы камни пролетали над стеной на высоте не менее 0,5 метра.
Грузовик перевозит партию песка массой 392 тонны, ежедневно увеличивая норму на одно и то же число тонн. За первый день было вывезено 2 тонны песка, а весь груз был перевезён за 16 дней. Сколько тонн было перевезено за двенадцатый день?
Найдите наибольшее значение функции [math]y=6\cos x-3x[/math] на [math]\left[0;\;\frac{\mathrm\pi}2\right][/math].
Часть 2.
При выполнении заданий 13—19 требуется записать полное решение и ответ.
а) Решите уравнение [math]8^{\frac23x-1}=11\cdot2^{x-3}-3[/math].
б) Найдите все корни этого уравнения, принадлежащие промежутку [1,75; 4).
Решение:
а)[math]8^{\frac23x-1}=11\times2^{x-3}-3[/math];
[math]2^{3(\frac23x-1)}=11\times2^{x-2}-3;[/math]
[math]2^{2x-3}=11\times2^{x-3}-3;[/math]
[math]8\times2^{2x-6}-11\times2^{x-3}+3=0;[/math].
Пусть [math]2^{x-3}=t,\;t>0[/math], тогда уравнение примет вид [math]8t^2-11t+3=0[/math]
[math]t_1=1;\;t_2=\frac38[/math]. Вернемся к замене: [math]2^{x-3}=1;\;x=3[/math];
[math]2^{x-3}=\frac38;\;x=\log_23[/math]
б) Очевидно, что [math]x=3[/math] принадлежит указанному промежутку и [math]\log_23<4[/math]
[math]\log_23\geq1,75[/math]; [math]\log_23\geq\frac74;[/math] [math]3\geq2^\frac74;[/math] [math]3^4\geq2^7;[/math] [math]81\geq128;[/math] неверно, значит [math]\log_23[/math] не принадлежит указанному промежутку.
Ответ: log23; 3; б) 3
В правильной треугольной призме ABCA1B1C1 косинус угла между прямыми АС1 и В1С равен 1/25.
а) Постройте сечение призмы плоскостью, проходящей через точки А и С1 параллельно прямой B1C.
б) Найдите площадь поверхности данной призмы, если её высота равна 6.
Решение:
а) Построим призму [math]ABCA_1B_1C_1[/math] и на продолжении стороны [math]BB_1[/math] возьмем точку [math]B_2[/math], как показано на рисунке, при этом [math]B_1B_2=BB_1[/math].
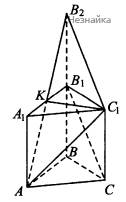
Заметим, что [math]B_1B_2С_1С[/math] - параллелограмм, поэтому [math]B_2C_1\parallel CB_1[/math]. Ясно, что точки [math]A_1,\;B_1,\;B,A,B_2[/math] лежат в одной плоскости. Рассмотрим плоскость [math](B_2C_1A)[/math]. Обозначим через [math]K[/math] точку пересечения прямых [math]A_1B_1[/math] и [math]B_2A[/math]. [math]\bigtriangleup AKC_1\;[/math] образует искомое сечение.
б) [math]AB=BC=AC=a\;[/math], тогда из прямоугольного треугольника [math]ACC_1[/math] получим [math]AC_1^2=a^2+36[/math]. Аналогично, из [math]\bigtriangleup B_1B_2C_1[/math] получим [math]B_2C_1^2=a^2+36[/math]. Ясно, что [math]BB_2=BB_1+B_1B_2=12[/math]. Из прямоугольного треугольника [math]AB_2B[/math] получим [math]AB_2^2=144+a^2[/math]. Заметим, что [math]\cos\angle B_2C_1A=-\frac1{25},[/math] так как угол [math]B_2C_1A[/math] - это угол между [math]\overrightarrow{C_1B_2}[/math] и [math]\overrightarrow{C_1A}[/math], а [math]\overrightarrow{C_1B_{2}}\;\uparrow\downarrow\;\overrightarrow{B_1C},[/math]
[math]\cos(\widehat{\overrightarrow{B_1C};\overrightarrow{C_1A}})=\frac1{25}[/math],
[math]\cos(\widehat{\overrightarrow{C_1B_2};\overrightarrow{C_1A}})=-\frac1{25}[/math]
Из [math]\bigtriangleup B_2AC_1[/math] по теореме косинусов:
[math]B_2A^2=B_2C_1^2+AC_1^2-2B_2C_1\times AC_1\times\cos\angle B_2C_1A[/math]
[math]a^2+144=a^2+36+a^2+36+2(a^2+36)\frac1{25}[/math]
[math]a=8[/math]
Последовательно найдем площадь боковой поверхности призмы ([math]3\times8\times6=144[/math]), площадь основания призмы [math]\frac{8^2\sqrt3}4=16\sqrt3[/math], площадь полной поверхности призмы [math]144+2\times16\sqrt3[/math]
Ответ: [math]144+32\sqrt3[/math]
Решите неравенство
[math]\frac{9^x-2\times3^{x+1}+4}{3^x-5}+\frac{2\times3^{x+1}-51}{3^x-9}\leq3^x+5[/math]
Пусть t= 3x, тогда неравенство примет вид:
[math]\frac{t^2-6t+4}{t-5}+\frac{6t-51}{t-9}\leq t+5;\;[/math]
[math]\frac{(t-1)(t-5)}{t-5}-\frac1{t-5}+\frac{6(t-9)}{t-9}+\frac3{t-9}\leq t+5;[/math]
[math]-\frac1{t-5}+\frac3{t-9}\leq0;\;[/math]
[math]\frac{t-3}{(t-5)(t-9)}\leq0,[/math]
Получим [math]3^x\leq3[/math] и [math]5<3^x<9,[/math]
Решение исходного неравенства: [math]x\leq1;\;\log_35<x<2[/math]
Ответ: [math](-\infty;1\rbrack;\;(\log_35;\;2).[/math]
Две окружности касаются внешним образом в точке K. Прямая AB касается первой окружности в точке A, а второй — в точке B. Прямая BK пересекает первую окружность в точке D, прямая AK пересекает вторую окружность в точке C.
а) Докажите, что прямые AD и BC параллельны.
б) Найдите площадь треугольника AKB, если известно, что радиусы окружностей равны 4 и 1.
а) Обозначим центры окружностей O1 и O2 соответственно. Пусть общая касательная, проведённая к окружностям в точке K, пересекает AB в точке M. По свойству касательных, проведённых из одной точки, AM = KM и KM = BM. Треугольник AKB, у которого медиана равна половине стороны, к которой она проведена, прямоугольный.

Вписанный угол AKD прямой, поэтому он опирается на диаметр AD. Значит, AD [math]\perp[/math] AB. Аналогично, получаем, что BC [math]\perp[/math] AB. Следовательно, прямые AD и BC параллельны.
б) Пусть, для определённости, первая окружность имеет радиус 4, а вторая — радиус 1. Треугольники BKC и AKD подобны, [math]\frac{AD}{BC}=4[/math]. Пусть SBKC = S, тогда SAKD = 16S. SAKB = SDKC = 4S, так как 4KB = AK и 4KC = KD
Вычислим площадь трапеции ABCD. Проведём к AD перпендикуляр O2H, равный высоте трапеции, и найдём его из прямоугольного треугольника O2HO1:
Тогда
Следовательно, 25S=20, откуда S=0,8 и SAKB = 4S = 3,2
Ответ: 3,2
Для перевозки большого числа ящиков по 130 кг и по 110 кг выделены двухтонные машины. Можно ли загрузить такими ящиками машину полностью? Укажите все варианты того, сколько ящиков каждого вида при этом можно взять.
Решение:
Обозначим через [math]x[/math] число ящиков по 130кг и через [math]y[/math] - число ящиков по 110 кг. Тогда должно выполняться [math]130x+110y=2000[/math], или [math]13x+11y=200[/math], где [math]x[/math] и [math]y[/math] могут быть только целыми положительными числами.
[math]x\geq0[/math], поэтому [math]11y\leq200,\;y\leq18[/math].
[math]y\geq0[/math], поэтому [math]13x\leq200,\;x\leq15[/math].
Далее у нас есть 2 пути.
1) Перебираем все значения [math]x[/math] от 0 до 15 и находим целые значения y.
2) Решим уравнение [math]13x+11y=200[/math] в целых числах.
[math]11y=200-13x[/math]
[math]y=18-x+\frac{2-2x}{11}[/math]
[math]y=18-x+\frac{2(1-x)}{11}[/math]
Так как [math]x,y[/math] целые, то [math]1-x[/math] делится на 11, [math]1-x=11k,\;k\in\mathbb{Z}[/math], [math]x=1-11k[/math], [math]y=\frac{200-13x}{11}=\frac{200-13(1-11k)}{11}=\frac{200-13}{11}+13k=17+13k.[/math]
Мы получили, что [math]\left\{\begin{array}{l}x=1-11k,\\y=17+13k\end{array}\right.k\in\mathbb{Z}.[/math]
[math]\begin{array}{l}x\geq0,\;1-11k\geq0,\;k\leq\frac1{11},\\y\geq0,\;17+13k\geq0,\;k\geq-\frac{17}{13}\end{array}[/math], значит, [math]k[/math] может быть равно [math]-1[/math] или [math]0[/math]
Если [math]k=-1[/math], то [math]x=12,\;y=4.[/math]
Если [math]k=0[/math], то [math]x=1,\;y=17.[/math]
Ответ: полностью машины можно загрузить, если в каждую машину установить 12 ящиков по 130кг и 4 ящика по 110кг или 1 ящик 130кг и 17 ящиков по 110кг
Найдите все значения параметра a, при которых уравнение [math](3-\;2\;tgx)^2\;(a^2+2a-4)(3-2tgx)\;+\;(a^2-1)(2a-3)\;=\;0[/math] имеет на отрезке [math]\left[-\frac{\mathrm\pi}2;\mathrm\pi\right][/math] ровно 2 решения.
Сделаем замену [math]3-2tgx=t,[/math] уравнение примет вид [math]t^2-(a^2+2a-4)t+(a^2-1)(2a-3)=0.[/math] пользуясь обратной теоремой Виета, запишем корни уравнения [math]t_1=a^2-1,\;t_2=2a-3[/math], откуда:
[math]\left\{\begin{array}{l}3-2tgx=a^2-1\\3-tgx=2a-3\end{array}\right.\;\left\{\begin{array}{l}tgx=\frac{4-a^2}2\\tgx=3-a\end{array}\right.[/math]
Изобразим эскиз графика функции [math]y=tgx[/math] при [math]x\in\left[-\frac{\mathrm\pi}2;\mathrm\pi\right][/math] (см. рисунок)
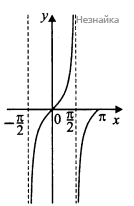
Очевидно, что при [math]x\in\left[-\frac{\mathrm\pi}2;\mathrm\pi\right][/math], уравнение [math]tgx=b[/math] имеет 2 решения при [math]b\leq0[/math]
и 1 решение при [math]b>0[/math]. Значит исходное уравнение на отрезке [math]\left[-\frac{\mathrm\pi}2;\mathrm\pi\right][/math] имеет ровно 2 решения в одном из 2 случаев.
1) [math]\frac{4-a^2}2=3-a\leq0[/math]
2) [math]\left\{\begin{array}{l}\begin{array}{c}\frac{4-a^2}2>0\\3-a>0\end{array}\\\frac{4-a^2}2\neq3-a\end{array}\right.[/math]
Рассмотрим каждый из этих случаев отдельно.
1) Решим вспомогательное уравнение [math]\frac{4-a^2}2=3-a;\;a^2-2a+2=0[/math] - нет корней.
2) Решим систему: [math]\left\{\begin{array}{lc}\begin{array}{c}\frac{4-a^2}2>0\\3-a>0\end{array}&\\\frac{4-a^2}2\neq3-a&\end{array}\right.[/math]
Из предыдущего пункта воспользуемся тем фактом, что уравнение [math]\frac{4-a^2}2=3-a[/math] не имеет решений. Получим систему [math]\left\{\begin{array}{l}4-a^2>0\\3-a>0\end{array}\right.[/math]. [math]a\in(-2;2)[/math]
Ответ: [math](-2;2)[/math]
На n деревьях, расположенных по окружности, сидели n весёлых чижей (на каждом дереве по чижу). Время от времени два чижа одновременно перелетают на соседние деревья в противоположных направлениях (один по часовой стрелке, другой — против). Могут ли все n чижей собраться на одном дереве, если
а) n = 3?
б) n = 2015?
в) n = 10?
Решение:
а) Занумеруем деревья числами 1,2,3 (по порядку). Пусть один чиж сидит неподвижно, например, на дереве 2, тогда чижи с деревьев 1 и 3, совершив по одному перелету, окажутся на дереве 2. Итак, все три чижа могут собраться на 1 дереве.
б) Пусть один чиж сидит неподвижно на дереве. Разобьем остальных чижей на пары, сидящих на одинаковом расстоянии [math]r[/math] перелетов от неподвижного в ту и другую сторону ([math]r=1,2,...,1007[/math]). Ясно, что каждая такая пара может за [math]r[/math] перелетов попасть на то дерево, где сидит неподвижных чиж.
в) Занумеруем деревья по порядку, например, по часовой стрелке числами от 1 до 10. Пусть количество чижей на [math]k[/math]-м дереве какой то момент времени равно [math]a_k[/math].
Посчитаем сумму [math]S_1=a_1+a_3+a_5+a_7+a_9[/math] - количество чижей на деревьях с нечетными номерами и сумму [math]S_2=a_2+a_4+a_6+a_8+a_{10}[/math] (с четными)
Если чижи перелетают с деревьев с нечетными номерами, то [math]S_1[/math] уменьшается на 2, а [math]S_2[/math] увеличивается на 2. Если чижи перелетают с деревьев с четными номерами, то получится тоже самое, только наоборот. Если же чижи перелетели с "четного" и "нечетного" деревьев, то суммы не изменятся. Видим, что четность [math]S_1[/math] и [math]S_2[/math] не меняется. Но если все чижи слетелись на одно дерево, то одна из сумм стала 10, а другая 0. В начале же [math]S_1=S_2=5[/math]. Суммы должны сохраняться нечетными, значит, такое невозможно
Ответ: а) да; б)да; в)нет.
| № | Ваш ответ | Ответ и решение | Первичный балл |
|---|---|---|---|
|
Здесь появится результат первой части. Нажмите на кнопку «Завершить работу», чтобы увидеть правильные ответы и посмотреть решения. |
|||